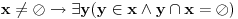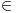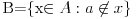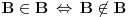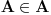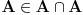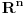Teorija skupova se izlaže aksiomatski. Najrasprostranjeniji sistem aksioma je ZFC. Teorija skupova se koristi i kao zasnivanje Matematike. Sistem ZFC na neki način opisuje "legalna" matematička sredstva. Ako se u dokazu koristi neko jače sredstvo, onda se mora istaći koje su dodatne hipoteze korišćene.
Aksioma separacije nam omogućava da iz bilo kog skupa izdvojimo podskup onih elemenata tog skupa koji imaju traženu osobinu izrazivu sredstvima predikatskog računa prvog reda na jeziku koji sadrži samo binarni relacijski simbol
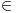
za pripadanje. Tako, ako bi A bio skup svih skupova, onda bismo mogli uočiti skup
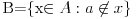
za koji bi važilo
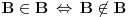
, što je kontradikcija. Dakle, Raselov paradoks u svetlu aksiomatske teorije skupova prestaje da bude paradoks i prelazi u teoremu da ne postoji skup svih skupova.
Prazan skup je skup bez elemenata. Ništa, pa ni prazan skup ne pripada praznom skupu.
Aksioma regularnosti tvrdi da je svaki neprazan skup disjunktan sa barem jednim svojim elementom. Iz nje sledi da ne postoji skup koji bi pripadao samom sebi. Naime, ako je A skup za koji važi da
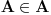
, onda bi skup {A} bio neprazan i njegov jedini element A ne bi bio disjunktan sa njim. Naime, zbog
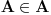
vaižlo bi
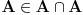
, odakle skupovi A i {A} ne bi bili disjunktni.
Skup {A} postoji z ma koji skup A po aksiomi para koja kaže da za ma koje a i b postoji skup čiji su jedini elementi a i b, tj. skup {a,b}, pa posebno kada je a=b=A dobijamo da mora da za ma koji skup A postoji skup {A}.
Kao što rekoh, ZFC je podrazumevano "radno okruženje" ako se ne kaže drugačije, ali se može raditi i sa drugim sistemima aksioma. Recimo, nekada matematičari dokazuju teoreme koristeći dodatne aksiome (i tada moraju da napišu šta su dodatno koristili) dokazujući tvrđenja koja se pomoću ZFC aksioma ne mogu niti dokazati niti opovrgnuti. Te dodatne hipoteze su takođe neka tvrđenja koja ne zavise od aksioma ZFC. Time se na primer u okruženju ZFC ispituju uzajamne veze između takvih hipoteza. Jedno od takvih napoznatijih tvrđenja je kontinuum hipoteza (CH) koja glasi:
"Ne postoji skup A takav da se niti skup R može 1-1 preslikati u skup A, niti da se skup A može 1-1 preslikati u skup N."
Sa druge strane, često se ispituju posledice samo nekog dela aksiomatskog sistema ZFC. Obično se u tim slučajevima "žrtvuje" aksioma izbora, koja se često zamenjuje nekim slabijim oblicima, tj. tvrđenjima koja slede iz aksioma ZFC, ali uz ostale aksiome teorije skupova (bez aksiome izbora) nisu ekvivalentna aksiomi izbora, već predstavljanju njene slabije oblike. OK, kada možemo ispitivati posledice sistema ZFC bez aksiome izbora (koji se označava sa ZF), zašto ne bismo ispitivali posledice aksioma teorije skupova bez aksiome regularnosti? Tada nećemo moći da dokažemo da nijedan skup ne pripada samom sebi. Sa druge strane, za aksiomu regularnosti se obično kaže da predstavlaj aksiomu "tehničkog karaktera", tj. nijedno bitno matematičko tvrđenje ne zavisi od aksiome regularnosti, već samo marginalne zavrzlame kao što je nepostojanje skupa koji bi pripadao samom sebi.
Nekada se aksioma izbora odbacuje i zamenjuje nekom od njenih slabijih oblika da bi se sistem aksioma proširio nekim važnim tvrđenjem koje protivreči sistemu aksioma ZFC. Dva najpoznatija takva tvrđenja su aksioma determinisanosti i Lebeg-merljivost svih podskupova skupa
.
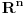
Nadam se da sam bio malo jasniji.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
Re: Moze li skup sadrzati samog sebe?
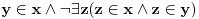jer da postoji takav z, on bi u isto vreme morao biti i skup i prirodan broj (babe i žabe).
