Srodne teme

21.01.2004. Zadatak sa opstinskog takmicenja
19.12.2004. Zabrana IP intervala
12.05.2005. generisanje slucajnih brojeva
26.06.2005. Jos jedan zadatak sa takmicenja...
22.11.2005. Lep zadatak .......
28.12.2005. Kalendar, podsjetnik, planer ili nesto trece...
09.01.2006. Least denominator
21.03.2006. jedan zadatak sa saveznog
25.02.2008. zadatak iz otpornosti
11.11.2006. Jos jedan zadatak iz C-a!

Navigacija

Brisanje liste

Lista poslednjih: 16, 32, 64, 128 poruka.

Zadatak sa pakovanjem vremenskih intervala

[es] :: Art of Programming :: Zadatak sa pakovanjem vremenskih intervala

Strane: 1 2 3 4

[ Pregleda: 9846 | Odgovora: 69 ] > FB > Twit

Autor

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
195.222.97.*

+2801 Profil

Zadatak sa pakovanjem vremenskih intervala

^{25.10.2008. u 10:06 - pre 200 meseci}

Vremenski trenutci su dati u obliku yyyy.mm.dd hh:mm:ss, pri čemu je yyyy u opsegu od 1901 do 2092. Potrebno je kodirati vremenske intervale (početak,kraj) sa samo 64 bita.

Napominjem da jedan trenutak nije moguće kodirati sa samo 32 bita.

_{[Ovu poruku je menjao Nedeljko dana 27.10.2008. u 09:50 GMT+1]}

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Miorot

Član broj: 195251
Poruke: 8
*.ptt.yu.

Profil

Re: Zadatak sa pakovanjem vremenskih intervala

^{25.10.2008. u 13:58 - pre 200 meseci}

Uzmimo npr. sledeću funkciju:

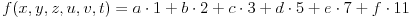
(1, 2, 3, 5, 7 i 11 su prvih šest prostih brojeva)
gde je:

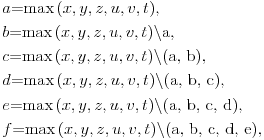
Primer: Datum 5.9.2007 11:28:49 (2007 = 1899 + 108) pamtimo kao

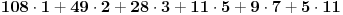
, tj. važna su nam dva sortirana niza (1, 2, 3, 5, 7, 11) koji je fiksiran i (2007, 49, 28, 11, 9, 5) koji se menja u zavisnosti od izabranog datuma.

Dakle, svaki datum funkcijom f preslikavamo u broj. Taj broj je jednoznačno određen, odnosno iz takvog jednog broja se ne može inverznom funkcijom funkcije f odrediti neki drugi datum, nego baš taj datum.
Zašto? Ima jedna teorema iz Algebre, ne sećam se koja, ali sećam se da ona tvrdi ovako nešto.
Inverzan postupak se, dakle, svodi na problem rastavljanja našeg broja na zbir 6 proizvoda

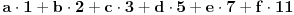
, odnosno određivanja x, y, z, u, v i t, a samim tim i potrebnog datuma.

Da vidimo koliko smo potrošili prostora za čuvanje ovakvih brojeva:

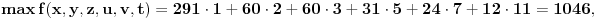
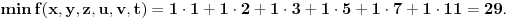
Uzimamo dakle opseg od 1 do 1018 (u postupku određivanja datuma ćemo dodati naknadno razliku 28).
Pošto čuvamo dva datuma

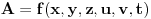
i

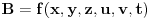
, to je onda

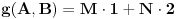
, gde su

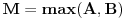
i

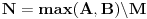
(g je nova funkcija po istom principu kao i f)
Dakle,

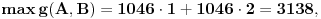
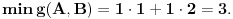
Uzimamo dakle opseg od 1 do 3136 (u postupku određivanja A i B ćemo dodati naknadno razliku 2).

Dakle,

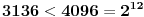
, odnosno, potrošili smo 12 bitova za čuvanje dva datuma.

Kako ćemo znati koji od (a, b, c, d, e, f) su naši (x, y, z, u, v, t)? Pošto podataka u vremenskom trenutku ima ukupno 6 (godina, mesec, dan, sat, minut, sekunda), za čuvanje informacije o sortiranom nizu podataka koristićemo za svaki podatak 3 bita, odnosno nisku od 18 bitova za jedan datum.
Za čuvanje redosleda podataka A i B dovoljno je koristiti nisku od dva bita.

To je ukupno 12+18+18+2=50 bitova. :-) (al' sam ga spalamudio...)

_{[Ovu poruku je menjao Miorot dana 25.10.2008. u 16:04 GMT+1]}

Odgovor na temu

mmix
Miljan Mitrović
Chief Software Architect
Financial Intelligence Software Ltd.
Passau, Deutschland

SuperModerator
Član broj: 17944
Poruke: 6050

+4631 Profil

Re: Zadatak sa pakovanjem vremenskih intervala

^{25.10.2008. u 14:29 - pre 200 meseci}

A sta cemo sa ova dva datuma:

31.12.2190 23:11:07
i
31.12.2190 23:07:11

oba imaju {a, b, c, d, e, f} = {291, 31, 23, 12, 11, 7} i f()=636 i isti je oba datuma iako se oni razlikuju, dakle f() nije "1-1" funkcija niti bi mogao da je rasclanis lepo jer su zadnja dva faktora = 11*7 + 7*11 i ne znas koji potice od kog clana. U prevodu ovo ti je lossy kompresija

Ovo je trik pitanje iz entropije, uzimajuci punu rezoluciju na nivou sekunde, opseg i prestupne godine (na to ste zaboravili), ukupan broj diskretnih jedinstvenih vrednosti za dva nezavisna datuma je:

86400 * (72*366 + 219*365) * 2 = 0x446B8ED00 (lakse je brojati bite u hex), dakle 64+3 = 67 bita. Slican metod (al u drugim opsezima) koristi Linux timestamp. U ovom sistemu nema redundantnih informacija i ne moze se "kompresovati" bez gubitka preciznosti. Osim ako neko ne zna neku magiju

Sloba je za 12 godina promenio antropološki kod srpskog naroda. On je od jednog
naroda koji je bio veseo, pomalo površan, od jednog naroda koji je bio znatiželjan, koji
je voleo da vidi, da putuje, da upozna,
od naroda koji je bio kosmopolitski napravio narod koji je namršten, mrzovoljan,
sumnjicav, zaplašen, narod koji se stalno nešto žali, kome je stalno neko kriv - Z.Đinđić

Odgovor na temu

Miorot

Član broj: 195251
Poruke: 8
*.ptt.yu.

Profil

Re: Zadatak sa pakovanjem vremenskih intervala

^{25.10.2008. u 15:07 - pre 200 meseci}

@mmix

Pogrešio sam na kraju, sada sam ispravio, potrebno je manje bitova. :-)

Citat:

mmix: A sta cemo sa ova dva datuma:

31.12.2190 23:11:07
i
31.12.2190 23:07:11

oba imaju {a, b, c, d, e, f} = {291, 31, 23, 12, 11, 7} i f()=636 i isti je oba datuma iako se oni razlikuju, dakle f() nije "1-1" funkcija niti bi mogao da je rasclanis lepo jer su zadnja dva faktora = 11*7 + 7*11 i ne znas koji potice od kog clana. U prevodu ovo ti je lossy kompresija ;)

Nije baš tako.

Za 31.12.2190 23:11:07 imamo 291*1+31*2+23*3+12*5+11*7+7*11=636 dok je niska za čuvanje redosleda oblika godina-dan-mesec-sat-minut-sekunda
Za 31.12.2190 23:07:11 imamo 291*1+31*2+23*3+12*5+11*7+7*11=636 dok je niska za čuvanje redosleda oblika godina-dan-mesec-sat-sekunda-minut

Funkcija jeste "1-1" u smislu da jednoj niski brojeva odgovara jedna vrednost, ali ove niske koje čuvaju redosled razlikuju dve funkcije sa istom vrednošću.

Odgovor na temu

Branimir Maksimovic

Član broj: 64947
Poruke: 5534
c-bg-d-p6-214.bvcom.net.

+1065 Profil

Re: Zadatak sa pakovanjem vremenskih intervala

^{25.10.2008. u 17:13 - pre 200 meseci}

U svakom slucaju mozes sa 64 bita da ukodiras range od 200 godina
tako sto bi pamtio "od" i "razliku".

Problem je u tome sto imas tri slucaja:
kad se "od" kodira sa 31 bit a razlika sa 33 bita.
kad se "od" kodira sa 32 bita a razlika sa 32 bita.
kad se "od" kodira sa 33 bita a razlika sa 31 bit.

E sad dakle da bi zadovoljio taj uslov potrebno je samo da
formiras tri niza, jedan za prvi, jedan za drugi, i jedan za treci slucaj.
Ukoliko hoces da range-ove ucitas sa nekog strima
potrebno je samo da prvi podatak u streamu bude tip niza i duzina.
i imas kompresiju, i gotovo. Dekodiranje je jednostavno
a imas i kompresiju ;)
ustedeo si dva bita po podatku ;)

Pozdrav!

Odgovor na temu

mmix
Miljan Mitrović
Chief Software Architect
Financial Intelligence Software Ltd.
Passau, Deutschland

SuperModerator
Član broj: 17944
Poruke: 6050

+4631 Profil

Re: Zadatak sa pakovanjem vremenskih intervala

^{25.10.2008. u 17:36 - pre 200 meseci}

To je

Citat:

Miorot:Nije baš tako.

Za 31.12.2190 23:11:07 imamo 291*1+31*2+23*3+12*5+11*7+7*11=636 dok je niska za čuvanje redosleda oblika godina-dan-mesec-sat-minut-sekunda
Za 31.12.2190 23:07:11 imamo 291*1+31*2+23*3+12*5+11*7+7*11=636 dok je niska za čuvanje redosleda oblika godina-dan-mesec-sat-sekunda-minut

Funkcija jeste "1-1" u smislu da jednoj niski brojeva odgovara jedna vrednost, ali ove niske koje čuvaju redosled razlikuju dve funkcije sa istom vrednošću.

To je ok, ali to je encoding, problem je kad radis decoding, imas samo rezultat f() i imas taj redosled, medjutim kad krenes da rasclanjujes f() na {a, b, c, d, e, f} imas problem sto f-ja nije "1-1" kad je dva ili vise od tvojih maximuma prost broj 1,2,3,5,7 ili 11.
U primeru koji sam pomenuo uzmi recimo da si rasclanio a, b, c, d i znas koliko su tacno, ostaje ti da rasclanis 154, sto je 7*11 + 7*11 (sad sam namerno ovako napisao jer je ultimativno komutativnost mnozenja ono sto ubija tvoju teoriju). Ti ces znati da je e sekunda a f minut (ili obrnuto) na osnovu 3bitnog koda redosleda, ali neces znati da li je {e, f} = {7, 11} ili je {11, 7}, samim tim tvoj decoding ima dva rezultata koji podjednako odgovaraju.

Sloba je za 12 godina promenio antropološki kod srpskog naroda. On je od jednog
naroda koji je bio veseo, pomalo površan, od jednog naroda koji je bio znatiželjan, koji
je voleo da vidi, da putuje, da upozna,
od naroda koji je bio kosmopolitski napravio narod koji je namršten, mrzovoljan,
sumnjicav, zaplašen, narod koji se stalno nešto žali, kome je stalno neko kriv - Z.Đinđić

Odgovor na temu

Branimir Maksimovic

Član broj: 64947
Poruke: 5534
c-bg-d-p6-214.bvcom.net.

+1065 Profil

Re: Zadatak sa pakovanjem vremenskih intervala

^{25.10.2008. u 18:10 - pre 200 meseci}

Znace jer je taj opis ujedno i sort odrer opadajuci.
Tako da ako ima da bira izmedju 7,11 i 11,7 izabrace
po sort redosledu. Ili sam nesto propustio?
Medjutim dekoding ovoga mnogo traje pa se ne isplati
to raditi po mom misljenju.

Pozdrav!

Odgovor na temu

mmix
Miljan Mitrović
Chief Software Architect
Financial Intelligence Software Ltd.
Passau, Deutschland

SuperModerator
Član broj: 17944
Poruke: 6050

+4631 Profil

Re: Zadatak sa pakovanjem vremenskih intervala

^{25.10.2008. u 18:54 - pre 200 meseci}

Primer nije dobar, poradicu na tome. Moram da stavim sve na papir, nek ostane to za sada.

Medjutim i ako uzmemo da je to ispravno, ovaj deo je problematican: g(A, B) = M + 2N za kompresiju dva datuma u 12 bita. Time efektivno dobijas linearnu jednacinu sa dve nepoznate (x + 2y = c) koja nije resiva jer je nepotpun sistem. Tako da moras da zadrzis tih 12 (zapravo 10) bitova po datumu plus oba poziciona niza.
Pride pozicioni niz od 6 elemenata moze da bude kraci od 18 bita. Tu imas 6! permutacija skupa {yy, mm, dd, h, m, s} ako sve permutacije indeksiras u istom pretku mozes da zapises svaku permutaciju brojem od 0 do 719 sto staje u 10 bita.

Tako da je zapravo 2 x (10 + 10) = 40 bita, ali pod uslovom da f()+pos transformacija radi, sto mi deluje veoma neverovatno zbog entropije (skup svih mogucih vrednosti datetime nije redundantan), tako da negde mora da popusti. Misli da problem definitivno lezi u f-1(int) => {a, b, c, d, e, f} samo da nadjem odgovarajuci kontra primer (ili problem lezi u tome da ne vidim redundantnost).

_{[Ovu poruku je menjao mmix dana 25.10.2008. u 20:05 GMT+1]}

Sloba je za 12 godina promenio antropološki kod srpskog naroda. On je od jednog
naroda koji je bio veseo, pomalo površan, od jednog naroda koji je bio znatiželjan, koji
je voleo da vidi, da putuje, da upozna,
od naroda koji je bio kosmopolitski napravio narod koji je namršten, mrzovoljan,
sumnjicav, zaplašen, narod koji se stalno nešto žali, kome je stalno neko kriv - Z.Đinđić

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
195.222.97.*

+2801 Profil

Re: Zadatak sa pakovanjem vremenskih intervala

^{25.10.2008. u 19:10 - pre 200 meseci}

Citat:

Branimir Maksimovic: Problem je u tome sto imas tri slucaja:
kad se "od" kodira sa 31 bit a razlika sa 33 bita.
kad se "od" kodira sa 32 bita a razlika sa 32 bita.
kad se "od" kodira sa 33 bita a razlika sa 31 bit.

Kada vršiš dekodiranje, ti imaš samo niz od 64 bita i nikakve dodatne informacije tipa "za ovo je korišćen 31 bit, a za ono 33 bita".

Citat:

Branimir Maksimovic: Znace jer je taj opis ujedno i sort odrer opadajuci.
Tako da ako ima da bira izmedju 7,11 i 11,7 izabrace
po sort redosledu.

Onda ne može da kodira 7,11, već samo 11,7. Šta ako je kodirao 7,11, a po sort redosledu dekodira 11,7? Neće dobiti isto što je kodirao. mmix je u pravu.

U opsegu od 192 godine sekundi ima 60*60*24*365.25*192 = 6,059,059,200 > 4,294,267,296 = 2³², pa je za kodiranje jednog trenutka potrebno 33 bita. Parova trenutaka ima 36,712,198,389,104,640,000 < 36,893,488,147,419,103,232 = 2⁶⁵, pa je za kodiranje dva trenutka potrebno 65 bitova. Međutim, nas ne zanimaju svi parovi, jer odbacujemo one kod kojih je početak posle kraja, a takvih je oko pola, pa je broj mogućih parova prepolovljen, odakle sledi da se može uštedeti jedan bit. To je bila caka!

Prebrojmo koliko ima parova (a,b) brojeva iz skupa {0,1,...,n-1} kod kojih je a<=b. Parova oblika (*,b) ima b+1 (to su parovi (0,b),...,(b,b)), pa pošto b može biti bilo koji od brojeva 0,...,n-1, sledi da je ukupan broj parova

. Kod nas je n=6,059,059,200, pa je ukupan broj intervala 18,356,099,197,581,849,600 < 18,446,744,073,709,551,616 = 2⁶⁴, pa se sve može (jedva) zgurati u 64 bita i ne može sa manje od 64. Na sličan način se izračunava da je za opseg od 193 godine nedovoljno 64 bita.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
195.222.97.*

+2801 Profil

Re: Zadatak sa pakovanjem vremenskih intervala

^{25.10.2008. u 19:18 - pre 200 meseci}

Miorot,

prvo, ne znam šta znači ovo:

Drugo, kako misliš iz vrednosti

da izračunaš

?

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

mmix
Miljan Mitrović
Chief Software Architect
Financial Intelligence Software Ltd.
Passau, Deutschland

SuperModerator
Član broj: 17944
Poruke: 6050

+4631 Profil

Re: Zadatak sa pakovanjem vremenskih intervala

^{25.10.2008. u 19:45 - pre 200 meseci}

Ok, zapravo je bilo jednostavnije nego sto sam mislio, potrebno je samo naci dva sorted {a, b, c, d, e, f} niza koji daju isti f() a za isti niz redosleda daju dva razlicita i smislena datuma.

Neka je niz redosleda za oba {yy, mm, dd, h, m, s}

1900-01-01 07:07:07 => {1, 1, 1, 7, 7, 7}, f=167
1900-01-01 01:05:11 => {1, 1, 1, 1, 5, 11}, f=167

tako da ti f+pos nije jednozacan. I sad kad nedeljko okaci zadnji post, u stvari se vidi i da je f-1 neresiv jer pokusavas da resis jednu jednacinu sa 6 nepoznatih bez sistema, kao posledica toga je i gornji primer.

BTW, nedeljko, imas onda problem u postavci zadatka posto nisi resio svoj zadatak

. Opseg koji si dao u prvom postu nije 192 godine vec 291 godinu

Pretpostavljam da je typo.

PS: Evo i dva descending sort niza sa istim f koji daju smislene datume:
f = 35
3 3 1 1 1 1
2 2 2 1 1 1

Sloba je za 12 godina promenio antropološki kod srpskog naroda. On je od jednog
naroda koji je bio veseo, pomalo površan, od jednog naroda koji je bio znatiželjan, koji
je voleo da vidi, da putuje, da upozna,
od naroda koji je bio kosmopolitski napravio narod koji je namršten, mrzovoljan,
sumnjicav, zaplašen, narod koji se stalno nešto žali, kome je stalno neko kriv - Z.Đinđić

Odgovor na temu

Branimir Maksimovic

Član broj: 64947
Poruke: 5534
c-bg-d-p6-214.BVCOM.NET.

+1065 Profil

Re: Zadatak sa pakovanjem vremenskih intervala

^{25.10.2008. u 19:47 - pre 200 meseci}

Citat:

Kada vršiš dekodiranje, ti imaš samo niz od 64 bita i nikakve dodatne informacije tipa "za ovo je korišćen 31 bit, a za ono 33 bita".

Pa vidi dal ces imati tri niza od po 64 bita clanova ili samo jedan ali sa po 66 bita clanova
upravo zavisi dal ces tu informaciju morati da ukodiras zajedno sa podatkom ili ne?
Ako to ukodiras sa podatkom onda ti za to treba vise od 64 bita,
a ako formiras tri niza koja ti nista vise u memoriji nece uzimati nego jedan
postigao si kompresiju a prakticno dobio isto.
Drugo kad nekom saljes stream onda mora da ima header svakako.
A u serijalizaciji su ti potrebna minimum dva podatka: tip i duzina,
(ukoliko druga strana ne zna redosled unapred i kad se radi o nizovima) tako da i tu nista ne gubis.
Ako hocemo da pricamo o realnom problemu i realnom resenju.

Citat:

Onda ne može da kodira 7,11, već samo 11,7. Šta ako je kodirao 7,11, a po sort redosledu dekodira 11,7? Neće dobiti isto što je kodirao. mmix je u pravu.

Pa lepo je objasnio opisna polja koja se kodiraju sa po 3 bita ujedno i predstavljaju opadajuci redosled.
Dakle ako je e,f onda je e vece od f i treba da bude 11,7 ako je f,e onda f treba da bude vece od e
i onda je opet 11,7
Dakle slucaj 7,11 se potpuno odbacuje posto je uslov dekodiranja da redosled opisa ujedno bude i opadajuci
sort order. Koliko sam shvatio.

Pozdrav!

Odgovor na temu

mmix
Miljan Mitrović
Chief Software Architect
Financial Intelligence Software Ltd.
Passau, Deutschland

SuperModerator
Član broj: 17944
Poruke: 6050

+4631 Profil

Re: Zadatak sa pakovanjem vremenskih intervala

^{25.10.2008. u 19:53 - pre 200 meseci}

Citat:

Branimir Maksimovic: Dakle slucaj 7,11 se potpuno odbacuje posto je uslov dekodiranja da redosled opisa ujedno bude i opadajuci
sort order. Koliko sam shvatio.

OK, eve ga:
f = 35
3 3 1 1 1 1 2003-03-01 01:01:01
2 2 2 1 1 1 2002-02-01 01:01:01

koristeci isti pozicioni niz.

Sloba je za 12 godina promenio antropološki kod srpskog naroda. On je od jednog
naroda koji je bio veseo, pomalo površan, od jednog naroda koji je bio znatiželjan, koji
je voleo da vidi, da putuje, da upozna,
od naroda koji je bio kosmopolitski napravio narod koji je namršten, mrzovoljan,
sumnjicav, zaplašen, narod koji se stalno nešto žali, kome je stalno neko kriv - Z.Đinđić

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
195.222.97.*

+2801 Profil

Re: Zadatak sa pakovanjem vremenskih intervala

^{25.10.2008. u 20:08 - pre 200 meseci}

Branimire,

To što pričaš sa hederom znači da negde pakuješ dodatne informacije, a to nije to. Potrošio si 66 bita. Ako ne veruješ, reci mi koliko ti prostora treba za serijalizaciju 8,000,000 takvih intervala. 64MB ili 66MB? Trebaju ti dve funkcije: encode koja prihvata trenuke, proverava validnost i vraća int64 i funkciju decode, koja prihvata int64 i vraća početak i kraj. Pritom, bilo koji validan interval kada se kodira, pa dekodira, treba da se dobije ono što je kodirano.

Citat:

mmix: BTW, nedeljko, imas onda problem u postavci zadatka posto nisi resio svoj zadatak ;). Opseg koji si dao u prvom postu nije 192 godine vec 291 godinu ;) Pretpostavljam da je typo.

Da, sad vidim da sam lupio. Mislio sam na 100 godina manje. Hvala. No, ipak sam dokazao da ne postoji rešenje za opseg od >=193 godine.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
195.222.97.*

+2801 Profil

Re: Zadatak sa pakovanjem vremenskih intervala

^{25.10.2008. u 20:13 - pre 200 meseci}

Ja ne znam o kom vi sortiranju pričate. Delovi datuma ne moraju biti sortirani. Trenutak 2007-12-31 17:45 33 je validan i mora ga biti moguće kodirati i pri dekodiranju dobiti baš njega. O kakvom odbacivanju pričate?

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
195.222.97.*

+2801 Profil

Re: Zadatak sa pakovanjem vremenskih intervala

^{25.10.2008. u 20:31 - pre 200 meseci}

Imam, u pogledu stepena kompresije, skoro optimalan algoritam za kompresiju nekih netrivijalnih skupova podataka, kao što su šahovske partije i šahovske pozicije, pa čak i metod za procenu ukupnog broja šahovskih pozicija (mada me mrzi da kodiram), pa sam čak mislio i da vas navedem na njega postupno, primerima, ali ne mogu toliko da visim po ES-u, morao bih dosta da piskaram. U dilemi sam, koliko to druge zanima i koliko se isplati trošiti vreme na takve gluposti.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

mmix
Miljan Mitrović
Chief Software Architect
Financial Intelligence Software Ltd.
Passau, Deutschland

SuperModerator
Član broj: 17944
Poruke: 6050

+4631 Profil

Re: Zadatak sa pakovanjem vremenskih intervala

^{25.10.2008. u 20:33 - pre 200 meseci}

Pretpostavka njegovog resenja je da je {a, b, c, d, e, f} sortiran nanize (to je bila svrha onih Max izraza za koje si pitao), nije bas matematicki pravilno definisao al sam skontao sta je hteo da kaze. Na stranu to nije ispravno.

Sloba je za 12 godina promenio antropološki kod srpskog naroda. On je od jednog
naroda koji je bio veseo, pomalo površan, od jednog naroda koji je bio znatiželjan, koji
je voleo da vidi, da putuje, da upozna,
od naroda koji je bio kosmopolitski napravio narod koji je namršten, mrzovoljan,
sumnjicav, zaplašen, narod koji se stalno nešto žali, kome je stalno neko kriv - Z.Đinđić

Odgovor na temu

Branimir Maksimovic

Član broj: 64947
Poruke: 5534
c-bg-d-p6-214.BVCOM.NET.

+1065 Profil

Re: Zadatak sa pakovanjem vremenskih intervala

^{25.10.2008. u 20:35 - pre 200 meseci}

Citat:

To što pričaš sa hederom znači da negde pakuješ dodatne informacije, a to nije to. Potrošio si 66 bita. Ako ne veruješ, reci mi koliko ti prostora treba za serijalizaciju 8,000,000 takvih intervala. 64MB ili 66MB?

Nedeljko jesi li ti glup ili se samo pravis? Oprosti ali ovo je debilno ocigledno.
Na bilo koju velicinu podatka overhead je ako recimo cuvas tip i duzinu u 32 bitnim intovima
64x3 == 192 bit-a fiksno.
Znaci na tvojih 8miliona ili 8ziliona overhead ti je uvek 192 bit-a na strimu .
U memoriji imas overhead u zavinosti od toga koliko je heavi niz.
U C++-u ti je overhead 2 pointera vise sto je 64 ili 128 bita u zavisnosti od
toga gde si kompajlirao.

Miljane:

Citat:

f = 35
3 3 1 1 1 1 2003-03-01 01:01:01
2 2 2 1 1 1 2002-02-01 01:01:01

3*3+3*5+1*7 == 9+15+7 == 31
2*3+2*5+2*7 == 6+10+14 == 30
Ili sam ja totalno otisao u aut ;(

Pozdrav!

Odgovor na temu

mmix
Miljan Mitrović
Chief Software Architect
Financial Intelligence Software Ltd.
Passau, Deutschland

SuperModerator
Član broj: 17944
Poruke: 6050

+4631 Profil

Re: Zadatak sa pakovanjem vremenskih intervala

^{25.10.2008. u 20:49 - pre 200 meseci}

Citat:

Branimir Maksimovic: 3*3+3*5+1*7 == 9+15+7 == 31
2*3+2*5+2*7 == 6+10+14 == 30
Ili sam ja totalno otisao u aut ;(

Po njegovoj postavci f(niz) = 1*a + 2*b + 3*c + 5*d + 7*e + 11*f, ne znam po kojoj formuli si dobio ovo gore.

1*3+2*3+3*1+5*1+7*1+11*1 = 1*2+2*2+3*2+5*1+7*1+11*1 = 35

Sloba je za 12 godina promenio antropološki kod srpskog naroda. On je od jednog
naroda koji je bio veseo, pomalo površan, od jednog naroda koji je bio znatiželjan, koji
je voleo da vidi, da putuje, da upozna,
od naroda koji je bio kosmopolitski napravio narod koji je namršten, mrzovoljan,
sumnjicav, zaplašen, narod koji se stalno nešto žali, kome je stalno neko kriv - Z.Đinđić

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
195.222.97.*

+2801 Profil

Re: Zadatak sa pakovanjem vremenskih intervala

^{25.10.2008. u 20:53 - pre 200 meseci}

U nizu od 8 miliona intervala nisu svi istog tipa, pa ti treba za svaki od njih treba još dva bita da bi znao kom od 3 tipa pripada (31+33 ili 32+32 ili 33+31). Ja te očigledno nisam dobro razumeo jer nemam pojma o kojih 64x3=192 bitova pričaš. U svakom slučaju, nešto ti ne valja ako tim postupkom opseg od 193 godine možeš da obuhvatiš sa 64 bita, jer to je nemoguće.

Ako bilo koji od 3 tipa kodiraš sa 64 bita, onda ti pri dekodiranju treba još i informacija o tipu, što je još 2 bita.

Možeš li ti da napraviš ovakve funkcije:

Citat:

Nedeljko: encode koja prihvata trenuke, proverava validnost i vraća int64 i funkciju decode, koja prihvata int64 i vraća početak i kraj. Pritom, bilo koji validan interval kada se kodira, pa dekodira, treba da se dobije ono što je kodirano.

Odgovor je da ili ne.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

[es] :: Art of Programming :: Zadatak sa pakovanjem vremenskih intervala

Strane: 1 2 3 4

[ Pregleda: 9846 | Odgovora: 69 ] > FB > Twit

Srodne teme

20.03.2007. Ljudi,hitno mi treba ovaj zadatak za takmicenje....
17.07.2007. Zadatak sa prijemnog
22.08.2007. [Zadatak] Intervali (sa z-trening.com)
10.10.2007. [Zadatak] Ucitavanje pozitivnih cijeli broj u dek..
31.10.2007. [Zadatak] Slucajni brojevi iz intervala od -1 do 1
21.01.2009. zadatak iz dif.jednacina
20.04.2008. hitnaa pomoc!!! logicki zadatak
05.07.2008. Trebaom Zadatak (C sharp)

Navigacija

Lista poslednjih: 16, 32, 64, 128 poruka.