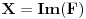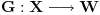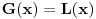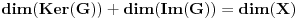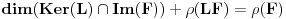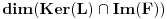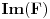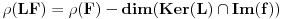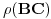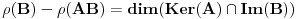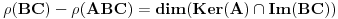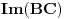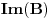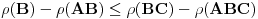• Naslovna
• FAQ
• Pravilnik
• O ES-u
• Tim
• Korisnici
• Statistike

 

• elitesecurity ::
• elitemadzone ::
• EMAIL ::
• RSS ::
• ES Mobile

  Niste ulogovani?  Username :   Password:   

• Registracija
• Zaboravili ste password?
• Flashback ▲▼
• Login problem?

 

Pretraga:

 

Srodne teme 05.11.2010. Vase misljenje o Counter Striku + par pitanja 07.09.2004. Zbirka zadataka za C#. 28.11.2009. Zadaci ( Crtanje Algoritama ) 30.05.2006. Zbirka zadataka sa rjesenjima u C/C++ 20.10.2005. Pomoc u vezi Algoritama 26.12.2005. ECDL problem oko zadataka za polaganje. 17.02.2006. par matematičkih zadataka 19.06.2006. Primena matrica i operacija nad njima 29.10.2006. Potrebna zbirka zadataka iz matematike. 17.05.2007. Par zadataka iz analize I Navigacija Brisanje liste Aktuelne teme u ovom forumu: Još jedan zadatak sa uglovima Treći zadatak sa uglovima Ostala rešenja algebarske jednačine Lep zadatak sa uglovima Najmanje pozitivno realno r Ikosaedar i gustina ms matematika.... Jedan zadatak sa pravouglim trouglom Japanese | Can you solve this ? | Math.. Jednakostraničan trougao Logaritamska nejednakost Raspoređivanje slova Košarkaši lep zadatak Zanimljiv zadatak o uglovima trougla Stado Boga Sunca ... 2000 godina star .. Izaberite forum: Linux Linux aplikacije Linux desktop okruženja Linux hardware Windows desktop Windows aplikacije Zaštita Office Windows drajveri Office :: Word Office :: Excel Macintosh Mac hardware Mac software Iphone Enterprise Networking SOHO Networking Wireless Windows mreže Linux mreže Wireless :: WiMax Wireless :: Mikrotik Wireless :: Wireless oprema Linux/UNIX serveri i servisi Unix BSD Skript jezici Security Virtualizacija Cloud Computing Services Security :: Kriptografija i enkripcija .NET 3D programiranje Art of Programming Asembler C/C++ programiranje Kernel i OS programiranje Pascal / Delphi / Kylix Java Embedded sistemi Perl PHP Python Visual Basic 6 Veštačka inteligencija Security Coding XML GameDev - Razvoj Igara Ostali programski jezici PHP :: PHP za početnike PHP :: Smarty template engine .NET :: .NET Desktop razvoj .NET :: ASP.NET .NET :: WPF Programiranje C/C++ programiranje :: C/C++ za početnike Baze podataka MySQL Oracle Access MS SQL Firebird/Interbase PostgreSQL Fiksna telefonija VoIP Udruženje korisnika teleko.. GSM - telefoni GSM - upotreba GSM - servisiranje Mreže i novosti Smartphone Mreže i novosti :: Mobilni internet Mreže i novosti :: Telenor - korisnički servis Mreže i novosti :: VIP - korisnički servis Mreže i novosti :: MTS - korisnički servis Smartphone :: Symbian OS Smartphone :: Windows Mobile Smartphone :: Android GSM - telefoni :: Nokia PDA Uređaji GPS Portable Players Anonimnost i privatnost ISP Browseri E-mail Instant Messaging FTP Google Hosting ISP :: Wireless mreže i ISP ISP :: ADSL E-mail :: Anti-spam Instant Messaging :: IRC Hosting :: Domeni Google :: Gmail E-Marketing Web aplikacije Web dizajn i CSS Web dizajn softver Web razvoj Pretraživači i SEO Flash Javascript i AJAX Web dizajn i CSS :: Kritike Grafički dizajn Izdavaštvo 3D modelovanje Rasterska grafika Vektorska grafika 3D modelovanje :: CAD/CAM Matične ploče, procesori .. Video karte i monitori Storage Ostali hardver Overclocking & Modding PC Konfiguracije Laptopovi Vodič za kupovinu - PC har.. Tablet PC Muzička produkcija Audio kompresija Audio softver Video produkcija Video kompresija Video softver Multimedijalni uređaji Digitalni fotoaparati Digitalne kamere Home Theater Digitalni fotoaparati :: Fotografija Digitalni fotoaparati :: Vodič za kupovinu - Digita.. Elektronika Elektrotehnika Elektronika :: TV uređaji Elektronika :: Radio elektronika i tehnika Elektronika :: Mikrokontroleri Elektronika :: Audio-elektronika Auto-elektronika :: Tuning Vodič za učenje Vodič za posao Vodič za emigraciju Fizika Matematika Nauka Sertifikati Informatika Vodič za učenje :: Seminarski radovi Vodič za učenje :: Obrazovne institucije Vodič za emigraciju :: Život u USA Vodič za emigraciju :: Život u Norveškoj Vodič za emigraciju :: Život u Nemačkoj E-Poslovanje E-Kupovina IT pravo i politika razvoja IT događaji IT berza poslova IS i ERP Ekonomija Berza Cryptocoins IT berza poslova :: Arhiva IT berze poslova IT pravo i politika razvoja :: Registar Nacionalnog ID E-Poslovanje :: E-Transakcije E-Poslovanje :: Forex E-Kupovina :: Platne kartice Digitalna Televizija Advocacy Ankete Predlozi i pitanja Vesti Čekaonica Vesti :: ES leto manifestacija MadZone TechZone Poljoprivreda AutoZone MotoZone Svakodnevnica Video igre MadZone :: Zanimljivi linkovi MadZone :: Kultura TechZone :: Ergonomija TechZone :: Grejanje TechZone :: Klimatizacija TechZone :: Bela tehnika AutoZone :: Fiat Panda club Lista poslednjih: 16, 32, 64, 128 poruka.

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 89.216.145.* +2801 Profil Par zadataka u vezi rangova. 30.09.2008. u 13:24 - pre 201 meseci Ja znam da su za Bojana ovi zadatak mačji dim i zato ga molim da ne objavljuje rešenje pre nego što drugi dobiju šansu da se oprobaju. Može posle da okači neko uopštenje ako hoće. Sa 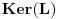označiću jezgro (kernel ili nula potprostor) linearnog preslikavanja sa 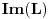njegovu sliku, sa 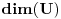dimenziju vektorskog (potprostora) i sa 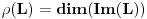rang linearnog preslikavanja . 1. Neka su 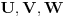vektorski prostori nad istim poljem skalara i neka su 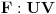i 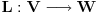i da je 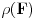konačan. Dokazati da je 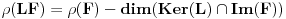. 2. Neka su 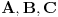takva linearna preslikavanja da postoji kompozicija 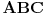i da je 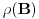konačan. Dokazati da je 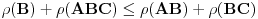. Naravno, isti rezultat automatski važi za rangove matrica koje se mogu množiti. Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.dynamic.sbb.rs. +2801 Profil Re: Par zadataka u vezi rangova. 02.10.2008. u 13:17 - pre 201 meseci Jel zadaci nisu interesantni ili niko ne ume da ih resi? Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.dynamic.sbb.rs. +2801 Profil Re: Par zadataka u vezi rangova. 03.10.2008. u 08:26 - pre 201 meseci Da li ovo ikoga uopšte zanima ili da ne objavljujem rešenja? Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

petarm Petar Mali Zrenjanin Član broj: 20220 Poruke: 1879 *.ns.ac.yu. +33 Profil Re: Par zadataka u vezi rangova. 03.10.2008. u 08:54 - pre 201 meseci Objavi resenja! Ocigledno trenutno nema previse zainteresovanih, ali bice sigurno za dan. dva... http://www.svijetfizike.com/ Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.dynamic.sbb.rs. +2801 Profil Re: Par zadataka u vezi rangova. 03.10.2008. u 13:31 - pre 201 meseci Možda ako se bar neko javi da je zainteresovan za rešenja. Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

petarm Petar Mali Zrenjanin Član broj: 20220 Poruke: 1879 *.adsl-a-1.sezampro.yu. +33 Profil Re: Par zadataka u vezi rangova. 04.10.2008. u 09:37 - pre 201 meseci Meni bi bilo zanimljivo da vidim resenja posto ne znam da resim ove zadatke. Ako su relativno detaljna naravno? http://www.svijetfizike.com/ Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 195.222.97.* +2801 Profil Re: Par zadataka u vezi rangova. 04.10.2008. u 18:41 - pre 201 meseci 1. Neka je i definisano sa . Poznata formula (zbir dienzija jezgra i slike jednak je dimenziji domena linearnog preslikavanja) daje . Obzirom da je po pretpostavci konačno, konačni su i i , pa je . 2. Iz konačnosti sledi konačnost , pa je , . Obzirom da je potprostor od , važi , odakle sledi tvrđenje. Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu