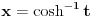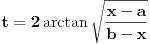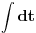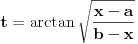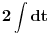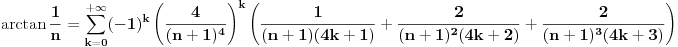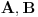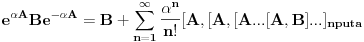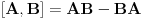Nedeljko je napravio previd znaka minus pod korenom. Neka su
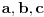 realni brojevi, pri čemu je
realni brojevi, pri čemu je 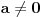 . Da bi podintegralna funkcija u kojoj se pojavljuje
. Da bi podintegralna funkcija u kojoj se pojavljuje 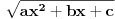 bila definisana na bar jednom intervalu, funkcija
bila definisana na bar jednom intervalu, funkcija 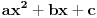 mora imati pozitivnu vrednost u bar jednoj tački, koju ćemo označiti sa
mora imati pozitivnu vrednost u bar jednoj tački, koju ćemo označiti sa  . Nadalje će
. Nadalje će  biti racionalna funkcija dve promenljive sa realnim koeficijentima, koja je definisana u bar jednoj tački realne ravni.
biti racionalna funkcija dve promenljive sa realnim koeficijentima, koja je definisana u bar jednoj tački realne ravni.Razmotrimo problem svođenja integrala
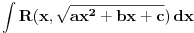 na integral racionalne funkcije.
na integral racionalne funkcije.Ako je
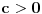 , onda se može koristiti druga Ojlerova smena:
, onda se može koristiti druga Ojlerova smena: 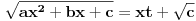 ,
, 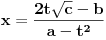 ,
, 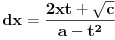 . Pomenuću i da je druga Ojlerova smena dovoljna za svođenje svakog integrala ovakvog tipa (bez obzira na znak broja
. Pomenuću i da je druga Ojlerova smena dovoljna za svođenje svakog integrala ovakvog tipa (bez obzira na znak broja  ) na integral racionalne funkcije, jer se nakon smene
) na integral racionalne funkcije, jer se nakon smene 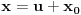 dobija integral na koji se može primeniti druga Ojlerova smena.
dobija integral na koji se može primeniti druga Ojlerova smena.Ako je
 , onda se može koristiti prva Ojlerova smena
, onda se može koristiti prva Ojlerova smena 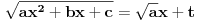 ,
, 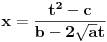 ,
, 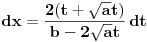 .
.Ako je
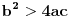 , to jest polinom
, to jest polinom 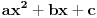 ima dve realne nule, koje ćemo označiti sa
ima dve realne nule, koje ćemo označiti sa 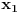 i
i 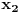 , recimo
, recimo  , onda se može koristiti treća Ojlerova smena
, onda se može koristiti treća Ojlerova smena 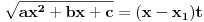 ,
, 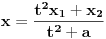 ,
, 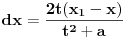 .
.U svakom slučaju, iracionalnost
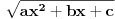 se uvek može linearnom smenom svesti na tačno jedan od sledeća tri oblika:
se uvek može linearnom smenom svesti na tačno jedan od sledeća tri oblika: 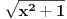 ,
, 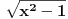 i
i 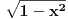 . U prvom slučaju se mogu koristiti smene
. U prvom slučaju se mogu koristiti smene 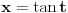 ,
, 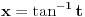 i
i 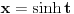 . U drugom slučaju se mogu koristiti smene
. U drugom slučaju se mogu koristiti smene 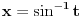 ,
, 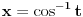 i
i 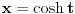 . U trećem slučaju se mogu koristiti smene
. U trećem slučaju se mogu koristiti smene 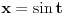 ,
, 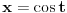 . Na taj način se dobijaju integrali koji se standardnim smenama svode na integrale racionalnih funkcija.
. Na taj način se dobijaju integrali koji se standardnim smenama svode na integrale racionalnih funkcija.



 Re: Zanimljivi zadaci - elegantna resenja
Re: Zanimljivi zadaci - elegantna resenja