[es] - Zanimljivi zadaci - elegantna resenja

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.mgnet.co.yu.

+33 Profil

Zanimljivi zadaci - elegantna resenja

^{17.07.2008. u 00:24 - pre 204 meseci}

Posto ima dosta ljudi na forumu mogli bi se i resavati zadaci! Da vidimo neka originalna resenja,ideje...

Evo jednog zadatka sa republickog takmicenja iz matematike za 4. razred gimnazije iz 1976. godine.

ZAD
Dokazati da je za svaki prirodan broj

http://www.svijetfizike.com/

Odgovor na temu

h4su

Član broj: 146153
Poruke: 162
80.65.165.*

+4 Profil

Re: Zanimljivi zadaci - elegantna resenja

^{17.07.2008. u 11:27 - pre 204 meseci}

Moze matematickom indukcijom lako da se rjesi.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.sbb.rs.

+2801 Profil

Re: Zanimljivi zadaci - elegantna resenja

^{17.07.2008. u 12:35 - pre 204 meseci}

Dokazati da je prvih

cifara iza decimalne tacke u zapisu broja

jednako 9.

Resenje je elegantno i dokumentovano na ovom forumu.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.mgnet.co.yu.

+33 Profil

Re: Zanimljivi zadaci - elegantna resenja

^{17.07.2008. u 17:02 - pre 204 meseci}

Citat:

h4su: Moze matematickom indukcijom lako da se rjesi.

To je jasno! Moze li bez nje? Neko originalno resenje?!

Citat:

Nedeljko: Dokazati da je prvih

cifara iza decimalne tacke u zapisu broja

jednako 9.

Resenje je elegantno i dokumentovano na ovom forumu.

Ovakve stvari su nepotrebne za bilo sta u nekoj praksi i zivotu pa se ne bih udubljivao! Ko ovo voli da radi iz hobija super!

http://www.svijetfizike.com/

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.dynamic.sbb.rs.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: Zanimljivi zadaci - elegantna resenja

^{18.07.2008. u 15:55 - pre 204 meseci}

Hajde da probam Petrov zadatak (ovaj koji je Nedeljko izneo sam upravo ja svojevremeno postavio na forum, pa nema smisla da opet pišem isto rešenje

).

Pođimo od identiteta

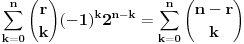
, za koji se lako vidi da važi za

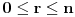
(tada su obe strane jednake

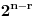
), ali kako obe strane predstavljaju polinom po

stepena najviše

, i kako se poklapaju u

tački, sledi da identitet važi uvek. Stavljajući sada

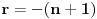
ostaje

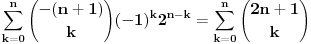
. Leva strana je jednaka

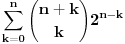
a desna predstavlja zbir prve polovine elemenata

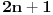
-og reda Paskalovog trougla, a kako su oni (zbog simetričnosti Paskalovog trougla) jednaki drugoj polovini, zbir na desnoj strani iznosi

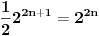
Deljenjem obeju strana sa

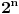
imamo identitet koji je trebalo dokazati.

Pao mi je na pamet i neki kombinatorni argument, ali o tom potom, kad proverim koliko to ima smisla. Naravno, bilo bi lepo zabeležiti i rešenje indukcijom, ali to bih prepustio nekom drugom.

_{[Ovu poruku je menjao Bojan Basic dana 11.03.2009. u 15:41 GMT+1]}

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.mgnet.co.yu.

+33 Profil

Re: Zanimljivi zadaci - elegantna resenja

^{19.07.2008. u 00:15 - pre 204 meseci}

Hajmo indukciju!

1.)

1=1

2.)

3.)

- ovo treba da se dobije nisam uspeo da ispetljam!

http://www.svijetfizike.com/

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.eunet.yu.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: Zanimljivi zadaci - elegantna resenja

^{19.07.2008. u 01:55 - pre 204 meseci}

Citat:

petarm:
3.)

Kud se dede

u binomnom koeficijentu?

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.mgnet.co.yu.

+33 Profil

Re: Zanimljivi zadaci - elegantna resenja

^{19.07.2008. u 02:26 - pre 204 meseci}

Greska! Ne treba da se dene!

http://www.svijetfizike.com/

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.eunet.yu.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: Zanimljivi zadaci - elegantna resenja

^{19.07.2008. u 12:55 - pre 204 meseci}

Dobro, ali sad ne možeš primeniti indukcijsku hipotezu.

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

Farenhajt
Goran Kapetanović
Beograd

Član broj: 78132
Poruke: 449
*.adsl.beotel.net.

+6 Profil

Re: Zanimljivi zadaci - elegantna resenja

^{19.07.2008. u 21:08 - pre 204 meseci}

Dokaz prvog zadatka preko verovatnoće:

Bacajmo novčić

puta. Tada izraz

predstavlja verovatnoću da u eksperimentu dobijemo

ishoda jedne vrste i

ishoda druge vrste. Eksperiment smatramo uspešnim ako se pojavilo

ishoda jedne vrste. To će se sigurno desiti posle najviše

bacanja (a eventualno i ranije). Dakle, sumiranjem navedenih izraza po

, u granicama od

, dobijamo siguran događaj, te suma iznosi

. Rezultat sledi.

EDIT: Desiće se, zapravo, posle

bacanja, po Dirihleu. Gde mi je greščica?

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.eunet.yu.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: Zanimljivi zadaci - elegantna resenja

^{19.07.2008. u 23:22 - pre 204 meseci}

Citat:

Farenhajt
...dobijemo

ishoda jedne vrste i

ishoda druge vrste.

Ovo je dvosmisleno: jesi li unapred fiksirao šta ti je jedna a šta druga vrsta, ili ti je pak bitno samo da odnos bude takav, bez obzira na to šta je šta? Ispravan je prvi rezon, tj. da kažemo „...dobijemo

pisama i

glava“, a ovo naglašavam zato što mi izgleda da si naknadno prešao na drugo tumačenje.

Svejedno, posle praviš mnogo veću grešku:

Citat:

Farenhajt:
Dakle, sumiranjem navedenih izraza po

Ovo ne možeš sumirati, jer su opiti različiti (bacaš

novčića, a

je promenljivo).

_{[Ovu poruku je menjao Bojan Basic dana 20.07.2008. u 03:28 GMT+1]}

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

Farenhajt
Goran Kapetanović
Beograd

Član broj: 78132
Poruke: 449
*.adsl.beotel.net.

+6 Profil

Re: Zanimljivi zadaci - elegantna resenja

^{20.07.2008. u 01:00 - pre 204 meseci}

A ovakvo tumačenje, recimo?

Stavimo

belih i

crnih kuglica u kutiju, pa nasumično izvučemo

kuglica. Eksperiment je "izvući sve bele kuglice", a nakon prvih

izvlačimo jednu po jednu dok se eksperiment ne okonča - a sigurno će se okončati najdalje do

-te kuglice.

EDIT: Tu je možda problem nezavisnost daljih izvlačenja. U tom slučaju, možda može ovako: Izvučemo

kuglica i konstatujemo jesu li među njima zastupljene sve bele. Ako nisu, vraćamo kuglice u kutiju i ponovo vadimo izvestan broj.

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.mgnet.co.yu.

+33 Profil

Re: Zanimljivi zadaci - elegantna resenja

^{20.07.2008. u 02:44 - pre 204 meseci}

Citat:

Bojan Basic: Dobro, ali sad ne možeš primeniti indukcijsku hipotezu.

Valjda ovako!

http://www.svijetfizike.com/

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.mgnet.co.yu.

+33 Profil

Re: Zanimljivi zadaci - elegantna resenja

^{20.07.2008. u 03:33 - pre 204 meseci}

ZAD
Neka su

neprekidne periodicne fje sa zajednickim periodom

, definisane na skupu realnih brojeva i neka je

. Dokazati da je

za svako

http://www.svijetfizike.com/

Odgovor na temu

h4su

Član broj: 146153
Poruke: 162
*.sa.hs-hkb.ba.

+4 Profil

Re: Zanimljivi zadaci - elegantna resenja

^{20.07.2008. u 12:39 - pre 204 meseci}

Mozel ovako kontrapozicijom:

Neka je f(t) razlicito od g(t) za neko t iz R.Tada je posto f i g imaju zajednicki period f(x+k*T) != g(x+k*T), k iz Z.Sada

.

P.S
Nisam siguran bas da je ona smjena korektna Petre.
Nemogu da nadjem link za 2 zadatak jel mozete okaciti ovdje.

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.eunet.yu.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: Zanimljivi zadaci - elegantna resenja

^{20.07.2008. u 14:27 - pre 204 meseci}

Citat:

Farenhajt:
Stavimo

belih i

crnih kuglica u kutiju, pa nasumično izvučemo

kuglica. Eksperiment je "izvući sve bele kuglice", a nakon prvih

izvlačimo jednu po jednu dok se eksperiment ne okonča - a sigurno će se okončati najdalje do

-te kuglice.

Ajd za nezavisnost, ali pri ovakvom eksperimentu nemaš

mogućih događaja.

Citat:

petarm:

Ne, naravno. Kada radiš nešto indukcijom, bitno je da prilikom pozivanja na indukcijsku hipotezu vrednost za koju je primenjuješ zaista bude manja od one s kojom tog momenta radiš — a ne samo da uvedeš smenu kako bi to tako izgledalo. :) U citiranom delu primenjuješ indukcijsku hipotezu za

(kako god ti to zvao, a nazvao si

), što ne možeš.

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.mgnet.co.yu.

+33 Profil

Re: Zanimljivi zadaci - elegantna resenja

^{20.07.2008. u 15:22 - pre 204 meseci}

I sad mozda iskoristiti Paskalovo pravilo

odnosno

i ovo opet ne mogu da ispetljam:(

http://www.svijetfizike.com/

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.mgnet.co.yu.

+33 Profil

Re: Zanimljivi zadaci - elegantna resenja

^{20.07.2008. u 20:03 - pre 204 meseci}

- fiksno

Ako je

parno ocigledno je i

parno i ako je

neparno onda je i

neparno! Pretpostavljam da je jedini nacin da pokazem kolko iznosi gornja suma je da pokazem kolko iznosi za

parno,

neparno i da pokazem da nema razlike? Voleo bih u svakom slucaju da vidim moze li se ovo ikako resiti drugacije?

- parno

- neparno

_{[Ovu poruku je menjao petarm dana 21.07.2008. u 13:30 GMT+1]}

http://www.svijetfizike.com/

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.mgnet.co.yu.

+33 Profil

Re: Zanimljivi zadaci - elegantna resenja

^{21.07.2008. u 00:28 - pre 204 meseci}

Zao mi je sto nisam uspeo da isteram ovo sa indukcijom do kraja. Voleo bih da neko drugi istera ako ima vremena da vidim gde sam gresio. A ja bih se iskupio na sledeci nacin
Ja sam dokazao upravo jednu matematicku relaciju koja se cesto koristi u fizici pa sam resio da je okacim ovde racunajuci da ce se nekom svideti.Uz to bice i prica uz ovaj dokaz!
To je operatorska relacija. U fizici se operatori pisu sa kapicom iznad slova ^ npr.

. To je uveo Landau (Nobelovac) kada je stigao u Moskvu. Stampari su u to vreme imali problema sa brojnim oznakama pa da bi im olaksao Landau je uveo da se operatori pisu na ovaj nacin.Fizicari tako pisu operatore i danas

. Bitni operatori za fiziku su linearni (za njih vazi princip superpozicije) i ermitski (predstavljeni su ermitskim matricama). Za takve operatore vazi identitet

Gde je

komutator (operatori su nekomutativne strukture) sa sledecim osobinama
http://www.elitesecurity.org/t330663-Osobine-komutatora

Ja cu pokusati da ovaj identitet dokazem matematickom indukcijom:

1.)

2.)

3.)

iskoristio sam jednu osobinu komutatora za koju vec postoji link u ovoj mojoj poruci

Poslednji sabirak je

-ti clan ove sume pa ga mogu uvuci pod sumu. Kada to uradim dobijam

Cime je ovaj identitet dokazan. Ako nekog zanima naglasio bih jos zasto je ova relacija vazna u fizici!
Za slucaj da

komutira sa

(naravno u tom slucaju komutira i sa svakim stepenom od

) u zapisu

dobija se

Posto se u kvantnoj mehanici postulira

lako se dobija

ili

Nadam se da se ovo nekom svidelo!

Ne znam Bojane dal mozda imas neku ideju kako bi se i ovo moglo dokazati bez indukcije?

http://www.svijetfizike.com/

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.sbb.rs.

+2801 Profil

Re: Zanimljivi zadaci - elegantna resenja

^{21.07.2008. u 08:30 - pre 204 meseci}

Citat:

petarm:

- fiksno

Ako je

parno ocigledno je i

parno i ako je

neparno onda je i

neparno! Pretpostavljam da je jedini nacin da pokazem kolko iznosi gornja suma je da pokazem kolko iznosi za

parno,

neparno i da pokazem da nema razlike? Voleo bih u svakom slucaju da vidim moze li se ovo ikako resiti drugacije?

Prvo,

. Račun ti nije tačan. Ne znam odakle ti

. A ako već znaš

možeš ga odmah primeniti na

.

Jedan način je školska formula za zbir aritmetičke progresije: prvi član plus poslednji član ima isti zbir kao drugi plus pretposlednji itd. Drugi način je da se

napiše kao

i onda ti se pokrate svi unutrašnji članovi. U vezi uopštenja ove ideje vidi

http://www.elitesecurity.org/p1997028

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu