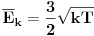Ima li potrebe za mernim jedinicama?

Voleo bih da procitate uvod iz Mehanike fluida profesora Stanoja Stojanovica.

UVOD

U mehanici, makroskopsko telo pod dejstvom sila koje na njega deluju, u opštem slučaju, vrši složeno kretanje. Ovo složeno kretanje se u osnovi može razložiti na translatorno pomeranje tela, njegovu rotaciju oko trenutne ose i deformaciju.
Često nas u pojedinim slučajevima ne interesuje ovakva opšta slika kretanja, već pojedini oblici ovog kretanja. Tako, za opisivanje pojava vezanih za translatorno kretanje uvodi se model materijalne tačke kojim se zamenjuje realno telo. Ili, za opisivanje pojava vezanih za rotaciono kretnje, realno telo se zamenjuje modelom apsolutno krutog tela. Međutim, za opisivanje pojava koje su posledica deformacije tela, nijedan od gornja dva modela nije dobar, već se mora uvesti treći model - model kontinuuma.
Kod deformabilnih tela rastojanja između molekula se menjaju pod dejstvom sila koje na njega dejstvuju. Pošto telo sadrži veoma veliki broj molekula (red veličine Avogadrovog broja 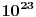), jasno je da ovakvi sistemi (tela) imaju vrlo veliki broj stepeni slobode. Čini se na prvi pogled da bi mehaniku ovakvih sistema mogli razvijati na bazi predstave o makroskopskom telu kao klasično-mehaničkom sistemu čestica. Međutim, u ovakvom prilazu postoji izvestan broj vrlo ozbiljnih problema. Prvi je, iako su sile među atomima elektromagnetne prirode, one su često nepoznate (ne zna se njihov analitički oblik). Drugi je, zbog veoma velikog broja atoma, broj dinamičkih jednačina je, takođe, veoma velik ( 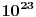), što, praktično, predstavlja nerešiv problem. Treći, čak i da možemo integraliti ovoliko veliki broj dinamičkih jednačina, određivanje integracionih konstanti, zbog principijelne nemogućnosti da istovremeno i tačno znamo položaj i brzinu svakog atoma u nekom početnom trenutku (početni uslovi), je nemoguće izvršiti. Međutim, čak i kada bismo mogli da nađemo konačne jednačine kretanja svih molekula, od ovakve detaljne slike ne bismo imali praktično nikakve koristi, jer bi prelaz na makroskopsku sliku zahtevao isuviše mnogo vremena. Prema tome, ovakav klasično-mehanički prilaz se ne može primeniti u analizi kretanja deformabilnih tela.
Međutim, nezavisno od prethodnog zaključka, nas po pravilu ne interesuje praćenje kretanja pojedinačno svakog atoma, već nas interesuje kako se menjaju makroskopske karakteristike deformabilnih tela.
Za makroskopsko proučavanje ovakvih sistema, koji sadrže veoma veliki broj čestica, koriste se dva opšta prilaza. Jedan od ovih opštih prilaza bazira na zakonima statističke fizike. U statističkom prilazu se polazi od realno postojeće situacije, odnosno od molekularne strukture sistema i sila koje vladaju među njima. Cilj je da se makroskopske karakteristike sistema objasne polazeći od osobina njegovih konstituenata (molekula) i njihove međusobne interakcije. Po pravilu, to obično nije moguće, već se osobine konstituenata kao i njihova međusobna interakcija aproksimiraju na pogodan način, da bi se mogla efektivno sprovesti teorijska analiza, odnosno da bi se odgovarajuće dinamičke jednačine mogle rešiti.
Drugi opšti prilaz u analizi kretanja sistema sa velikim brojem čestica je fenomenološki, ili makroskopski metod. On bazira na fenomenološkoj teoriji u kojoj se razmatraju zakoni koji povezuju makroskopske (makrofizičke) karakteristike sistema. Do ovih zakonitosti se dolazi ili empirijski, ili na osnovu opštih principa (na primer, zakona održanja energije i njemu sličnih), koji su u krajnjem posledica iskustva. Fenomenološka teorija predstavlja efektivan metod za rešavanje mnogih važnih praktičnih problema. U ovom kursu mi ćemo koristiti fenomenološki prilaz u proučavanju kretanja deformabilnih sredina.
U osnovi fenomenološke analize kretanja deformabilnih sredina leži aproksimacija po kojoj se stvarni diskretni raspored masa u njima zamenjuje kontinuumom, odnosno uzima se da su makroskopske karakteristike ovih sredina neprekidne funkcije prostornih koordinata i vremena. Ilustrujmo ovo na primeru vazduha. Pri normalnim uslovima (temperatura 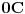i atmosferskom pritisku na nivou mora) u jednom 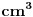vazduha ima 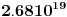molekula. Ako u ovoj zapremini uzmemo kocku čija je stranica 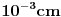, što je često unutar tačnosti merenja dužine u praksi, u njoj će se nalaziti 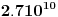molekula vazduha. Prema tome, ogromno mnogo molekula se nalazi čak i u veoma malim zapreminama, zbog čega se približno, a istovremeno i zadovoljavajuće tačno, može smatrati da je masa tela raspoređena kontinualno, odnosno na neprekidan način. Zahvaljujući ovoj idealizaciji (aproksimacija kontinuuma) pri proučavanju kretanja deformabilnih tela možemo koristiti matematičku analizu neprekidnih funkcija, diferencijalni i integralni račun, što u mnogome olakšava analizu ovih kretanja. U ovom smislu, mi ćemo u buduće deformabilna tela zvati neprekidnim sredinama.

---

Priroda je vec sama dovoljno komplikovana i ti Mikky ne mozes da stignes na more ni avionom, a kamoli puzeci!

---

Nedeljko je u prvoj poruci izneo tezu:
..ne postoji nikakva esencijalna potreba za mernim jeinicama, već eventualno praktična..
A kasnije još i ovo:
E, sad ide ono glavno. Merne jedinice imaju svoje definicije, to jest, ne spadaju u osnovne, već u izvedene pojmove. …

…. Dakle, pošto spadaju u izvedene pojmove, uvek se mogu eliminisati, to jest, sve što može sa njima, može i bez njih.

Ja mislim da nije tako.A evo zašto:
Da bi algebarski opisali neki fizički zakon moramo:a) Fizikalne pojmove izraziti brojevima.
b)Napraviti idealizirani model te pojave.
(Inače ne ide)
**Da bi fizičke pojmove izrazili brojevima moramo uvesti jedinicu mjere.
(Inače ne ide)
Mjerni broj nije neimenovan već imenovan.Imenovanjem (jedinicom mjere) ujedno
navodimo i karakter fizikalnog pojma.
Pokazalo se da se ovako opisani zakoni mogu kombinovati i razrađivati dalje po jasnim
pravilima matematike.Eksperimentalna fizika je potvrđivala matematička predviđanja.
----------------------------- ** jedinice mjere su standardizovane iz praktičnih razloga.
**JM je definisana pomoću etalona.
** JM i etalon mjere su različiti pojmovi.Naprimjer za metar je etalon-« najbolji atomski
sat i brzina svjetlosti», a za masu nekakav uteg u Parizu.
SI sistem nije racionaliziran matematički nego tehnološki.Zato imamo neke osnovne
jedinice mjere koje bi se mogle izraziti i pomoću drugih osnovnih jedinica.Naprimjer
stepen kelvina bi mogli izraziti metrom i sekundom,ali kako bi baždario termometar?
Mjeriti prosječne brzine atoma nekakvim mikrskopom?Ne.Bolje je ovako kako je usvojeno.

---

Neki očigledno nisu pažljivo čitali moje poruke.

Ako ja kažem da je dijagonala mog monitora 17, to zaista ne znači ništa, ali ako kažem da je n puta kraće od rastojanja Mesec-Zemlja, gde je n tačno određeni broj, onda sam ja izrazio veličinu mog monitora. Da bi izrazio odnos dve veličine isog karaktera (obe dužine ili obe snage itd.) ne treba mi nikakva merna jedinica, a to je jedino što zaista mogu da izrazim. Kada kažem da je dijagonala mog monitora 17 inča, izrazio sam odnos dijagonale mog monitora i rtalona inča, baš kao što sam dijagonalu monitora mogao da izrazim i preko odnosa sa rastojanjem od Zemlje do Meseca. Međutim, izražavanje u inčima je praktičnije jer se na svakom ćošku može kupiti instrument za merenje dužine u inčima (ili u metrima, pa da se izvrši konverzija).

Sa druge strane, ako se definicija ne može eliminisati iz svih iskaza i svih dokaza, onda ta definicija nije korektna. Drugim rečima, ako je merne jedinice nemoguće eliminisati, onda ih je nemoguće i definisati.

---

Nedeljko.Da bi izrazio odnos dve veličine isog karaktera (obe dužine ili obe snage itd.) ne treba mi nikakva merna jedinica, ....

Pa tu već imaš mjernu jedinicu.Jednu veličinu izražavaš pomoću omjera sa drugom.
Ova druga ti je mjerna jedinica i mora biti definirana.


Sa druge strane, ako se definicija ne može eliminisati iz svih iskaza i svih dokaza, onda ta definicija nije korektna. Drugim rečima, ako je merne jedinice nemoguće eliminisati, onda ih je nemoguće i definisati.

Dakle nešto kao svođenje na aksiome u matematici.
SI sistem sa 6 osnovnih mjernih jedinica bi se mogao mat.racionalizacijom svesti na samo dvije.A ove dvije (za vrijeme i masu) bi se definirale sa nekoliko postulata (aksioma fizike).Postulati su iskustveno uočeni i smatraju se vremenski nepromjenjivim pojmovima.
Zamjena standardne mjerne jedinice postulatima na kojima počiva je moguća.Tako se
obično radi u labaratorijama pri izvođenju eksperimenata.

---

A kolko je rastojanje izmedju Zemlje i Meseca?

---

@petarm

Ja tvrdim da se rastojanje izmedju Zemlje i Meseca ne može izraziti bez poređenja sa nekom drugom dužinom, tako da bi na to pitanje ti trebao da daš odgovor. Jeli Petre, koliko je rastojanje između Zemlje i Meseca?

@zzzz



Znači, svaka moguća dužina je merna jedinica za dužinu, budući da mogu govoriti o odnosu bilo koje dve dužine. Rastojanje između bilo čega bilo čega je merna jedinica za dužinu. Zanimljivo. Po tome ispada da je merna jedinica = veličina. OK, zašto se onda uvodi još jedan termin (merna jedinica) za isti pojam (veličine)? Još će da ispadne da su merne jedinice izmišljene da bi nam zakomplikovale život, a ne da bi nam ga olakšale.



SI sistem ima 7 osnovnih jedinica (Kg,m,s,mol,K,A,cd), a ostale su izvedene (m/s, cm, s²,...). No, ja ne govorim o osnovnim i izvedenim jedincama, već o osnovnim i izvedenim pojmovima. Jedinicu kao pojam možeš svoditi na druge jedinice, a možeš i opštije, da je kao pojam svodiš na druge pojmove (koji ne moraju biti jedinice). Osnovni pojam je pojam koji se ne definiše, a izvedeni je onaj koji ima definiciju. U SI sistemu postoje definicje sedam osnovnih mernih jedinica.

---

Ja bih rekao, merna jedinica = etalon veličine (fizičke dimenzije). Način izražavanja količine neke dimenzije, pa tako zaista čisto praktične upotrebne vrednosti. Onda različite jedinice imamo prosto jer je mozgu lakše da upoređuje brojeve s malo značajnih cifara, recimo do tri. Gde je neophodno brzo delovanje obično se jedinice podrazumevaju; npr. kad nešto ručno merimo u laboratoriji, obično izvikujemo samo brojeve, jer se jedinica podrazumeva: „Protok 17, pritisak 158!“ misleći na litre u sekundi i kilopaskale.

Tako da su merne jedinice tu zaista da bi nam olakšale život, gde mi = inženjeri. S druge strane, prema ličnom iskustvu, matematičarima je najbolje ispostavljati jednačine u bezdimenzionom obliku :) Matematičar koji radi u korist inženjerskog problema uopšte ne mora da se bakće s jedinicama. Tako su vuci siti i koze na broju.

Ali, rekao bih da je navođenjem jedinice mnogo bitnije to što se posredno ukazuje na fizičku dimenziju, ono na šta su Makraken i Fitopatolog zapravo ukazivali pominjanjem baba i žaba i provere formula. Posebno pritom mislim na Bakingemovu π-teoremu; npr. svaki pravi vazduhoplovac zna da avion leti zbog Bakingemove π, a da je sve ostalo nagvaždanje fizičarâ :)

Nedeljko : U SI sistemu postoje definicje sedam osnovnih mernih jedinica.

Ima gotovo 30 godina kako metar nije osnovna jedinica SI.A i onaj etalon-šipka je otišao u muzej.Usvojena je brzina svjetlosti c=299 792 458 m/s i zaleđena.Nema više još preciznijeg mjerenja c.
Gotovo je s tim.Metar je izvedena vrijednost iz ovog broja i etalona sekunde.
Potrudi se da shvatiš o čemu je riječ.
(Prikačio sam nešto uz prošlu poruku.)

Ja tvrdim da se rastojanje izmedju Zemlje i Meseca ne može izraziti bez poređenja sa nekom drugom dužinom

??? Osim ako se ne poredi sama sa saobom.Tada bi to rastojanje bilo mjerna jedinica (zm), a udaljenost Zemlja Mjesec: l= 1 (zm).

Znači, svaka moguća dužina je merna jedinica za dužinu, budući da mogu govoriti o odnosu bilo koje dve dužine. Rastojanje između bilo čega ** merna jedinica za dužinu. Zanimljivo. Po tome ispada da je merna jedinica = veličina.

a)Da ako je neko usvoji i definiše.
b)Isto kao pod a)
c)Da!I dali smo joj modul 1!
----------------------
Astronomi vole da udaljenost Sunce-Zemlja uzmu za jedinicu (L(s-z)=1), pa onda okolo mjere sa tom dužinom.A neki opet vole da im je put svjetlosti za godinu dana
jednak 1.Šta možemo kad ima svakakvih ljudi.

ČaslavJa bih rekao, merna jedinica = etalon veličine (fizičke dimenzije)

Ponekad da, ali ne uvijek.Obično etalon služi za baždarenje mjernih instrumenata
tj. mjerne jedinice.To je zakonom propisano.Imamo etalon etalona, pa i unuče etalona
sa potrebnim pedigreom i papirima.(Državni zavodi za mjere utege i dragocjenosti.)

---

Znam da je metar definsan preko brzine svetlosti i sekunde. No, on se i dalje smatra osnovnom jedincom SI sistema.

http://en.wikipedia.org/wiki/International_System_of_Units#Units

Ljudi su se jednostavno dogovorili da u izrazu m/s ne vrše skraćvanje, to jest, da brzina nije bezdimenziona veličina, a moglo bi i tako.

Na isti način kao što možeš metar da definišeš preko brzine svetlosti i sekunde, mogao bi da definišeš i kilogram preko, metra, sekunde i gravitacione konstante, a pošto je metar prethodno sveden na sekundu, da svedeš i kilogram na sekundu.

Slično, kelvin možeš predstaviti kao m²/s² puta neki broj (bezdimenziona veličina), jer je temperatura idealnog gasa ništa drugo do mera ukupne kinetičke energije čestica od kojih se gas sastoji po masi tog gasa.

Amper možeš definisati kao džul podeljen sa naelektrisanjem jednog elektrona i ponmožen sa nekom bezdimenzionom jedinicom.

No, ljudi su se dogovorili da između tih mernih jedinica ne vrše skraćivanje. Sa druge strane, dogovorili su se da za tromu i tešku masu koriste istu jedinicu, dok neko ne utvrdi postojanje razlike.



Upravo je to suštinski uslov da nešto bude merna jedinica. Ali, ja mogu da poredim bilo koje dve dužine, čak i ako nijedna od njih nije dogovorena jedinica (bez dogovora nema ni jedince).

---

@Nedeljko
Znači, svaka moguća dužina je merna jedinica za dužinu, budući da mogu govoriti o odnosu bilo koje dve dužine. Rastojanje između bilo čega bilo čega je merna jedinica za dužinu. Zanimljivo. Po tome ispada da je merna jedinica = veličina. OK, zašto se onda uvodi još jedan termin (merna jedinica) za isti pojam (veličine)? Još će da ispadne da su merne jedinice izmišljene da bi nam zakomplikovale život, a ne da bi nam ga olakšale.


Nije tako. Ali svaku duzinu mozes uzeti kao mernu jedinicu za duzinu. U zavisnosti od potrebe. Zato se u astronomiji uzima npr. parsek.

---

Ama, taj citat se odnosi na zzzz-ovu izjavu i ne može se izvaditi iz tog konteksta. Naravno da svaku dužinu možemo izabrati za mernu jedinicu, ali isto tako možemo i bez ikakve merne jedinice za dužinu, već da govorimo isključivo o odnosima dužina, koji ne zavise od izbora mernih jedinica.

---

Da je „problem“ upoređivanja veličina (jedinice, transformacija mjernih brojeva,...) bio obrazložen i povezan sa STR (posebno vezano za frekvencije, talasne dužine i „unutrašnje“, „sopstveno“ vrijeme vezano za brzinu svjetlosti i talasne dužine, te miješanje „baba i žaba“ u Lorencovim formulama, „kvadrivektorima“- matricama) vjerovatno bi diskusija u ovoj temi bila bogatija i sadržajnija.
U pokušaju da podstaknem diskusiju probao sam (ovdje) ubaciti formule, ali mi to (ponovo) ne ide.

za pocetak ovo nije tacno ;)

---

Ali ti si ovde iskoristio jedinicu... ili ako hoćeš etalon, ali tvoja jedinica nije standardna. Njen naziv glasi "visina mog prozora".

Korišćenje jedinica nije ništa drugo nego poredjenje sa etalonom odredjenog naziva.

Dakle...

---

Ovo što cicika kaže je OK.To je već ranije spomenuto.Ali da se podsjetimo na start:
Nedeljko je rekao: "Raspravljao sam se sa kolegama na poslu i nikako da ih ubedim da ne postoji nikakva esencijalna potreba za mernim jeinicama, već eventualno praktična, pa me zanima kako drugi razmišljaju o tome.

Kada kažem da je dijagonala mog monitora iznosi 0.432 m, ja sam zapravo izrazio odnos dveju dužina: dijagonale mog monitora i etalona metra. Taj iskaz se u suštini ne razlikuje od iskaza: dijagonala mog monitora je 3 puta kraća od visine mog prozora. Jedino što zaista mogu izraziti je odnos između dve dužine, bez obzira da li je imenilac neki dogovoreni etalon ili neka druga dužina, a da bih izrazio odnos između dveju dužina, ne treba mi nikakav sistem mernih jedinica. Rezultat je čist realan broj bez dimenzije, koji ne zavisi od izbora mernih jedinica."

A nešto kasnije spominje i mjerenje uglova (radijan).Izgleda da je on baš tu zalutao,
jer za mjerenje ugla stvarno je nepotrebno uvoditi jedinicu za mjerenje dužine.
Lijep logički zaključak:
1)Ugao je omjer dužine luka i dužine radijusa koji ga opisuje.(Pa onda slijedi:)
2)Bez obzira koji etalon mjere koristili, ovaj omjer će biti uvijek isti..(Pa onda slijedi:)
3)Etalon mjere nam ne treba, a ako ga neko već koristi to je samo iz praktičnih razloga.
.(Pa onda slijedi:)
4)Omjer između dvije dužine se može uzraziti brojem, a da se te dužine prethodno i ne mjere standardnim etalonom dužine..(Pa onda slijedi:)
5)Ima li potrebe za mjernim jedinicama?


NE, misli Nedeljko.

---