Pošto kažeš da ti jedino nije jasno zašto važi onakva relacija za jačinu polja, samo to ću ti pokazati. Vrlo je jednostavno. Posmatrajmo jednu beskonačno dugu nit sa dužinskom gustinom naelektrisanja
. Gausova teorema tvrdi da je
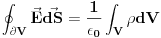
. Pošto problem ima aksijalnu simetriju uvodimo cilindrične koordinate, pri čemu se z-osa poklapa sa pravcem niti i pravimo par obzervacija. Ukoliko zarotiramo provodnik oko svoje uzdužne ose dobijamo fizički identičnu situaciju što znači da polje ne sme zavisiti od
koordinate, štaviše, ako transliramo provodnik duž z-ose, opet imamo fizički identičnu situaciju tako da polje ne sme zavisiti ni od z-koordinate, tako da važi
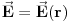
. Takođe, ove dve simetrije dozvoljavaju da polje ima i pozitivne i negativne
i
komponente. Ovakva nejednoznačnost nije dozvoljena tako da one moraju biti nula, što na kraju daje
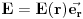
. Neka sada "kontrolna" zapremina koja figuriše u integralu na desnoj strani Gausove teoreme bude cilindar visine h i poluprečnika R sa osom koja se poklapa sa z osom. Ovaj integral je u stvari naelektrisanje obuhvaćeno "kontrolnom" zapreminom i ono iznosi
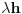
. Pozabavimo se levom stranom
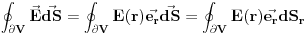
, gde je
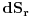
element površine omotača "kontrolne" zapremine (normale osnova su bile normalne na pravac polja tako da su nestale u skalarnom proizvodu, a normala omotača je paralelna sa pravcem polja tako da su se samo pomnožili). Kako je
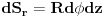
, sledi da je
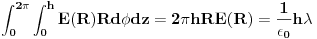
. Kako je R bilo proizvoljno, rešavanjem prethodne jednačine po E se dobija
.
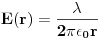
Eto, bio sam detaljan i nadam se jasan. U principu, na ovaj način rešavaš i probleme sa ostalim simetrijama.
Pomoc oko problema iz elektrostatike!
Registrovani: 1 ( BlackForce )