Ne treba ti teorema likova da bi resio ovaj zadatak.
Citat:
Omnicali: Polje u odredjenoj tacki povrsi racunas tako sto vektorski saberes polja pojedinacnih naelektrisanja sto bi trebalo da znas kako se radi.
Ali u zadatku se trazi indukovano povrsinsko naelektrisanje a ne jacina polja.
Citat:
petarm: 1.)Tackasto naelektrisanje q nalazi se na rastojanju l od beskonacne provodne ravni. Naci povrsinsku gustinu indukovanog naelektrisanja na ravni:
a)u tacki najblizoj naelektrisanju q
Prvo treba primetiti da tu provodnu ravan mozes zameniti za provodni poluprostor. Zasto? Zato sto se u provodniku nikada ne nalazi nikakvo naelektrisanje vec samo na povrsini pa onda taj deo poluprostora ne moze da utice na raspodelu naelektrisanja na povrsini.
Sada uzmes i zamislis mali valjak kao na sliici.
Na desnoj strani valjka ne postoji nikakvo elektricno polje jer se nalazi u provodniku. Sada zamislimo da je ta desna povrsina valjka jako blizu povrsini provodnika i da je precnik valjka mali. Posto je ta povrsina valjka blizu povrsine provodnog poluprostora onda ono povrsinsko naelektrisanje koje nije u valjku daje samo tangencijalnu komponentu elektricnog polja dok povrsinsko naelektrisanje u valjku daje normalnu komponentu i ta komponenta
iznosi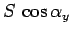 
. To mora da se potre sa elektricnim poljem od tackastog naelektrisanja E=1/(4Pi*Epsilon) * q/l^2 i tako nadjes Sigma.
b)u tacki koja se nalazi na rastojanju r od naelektrisanja
Tu uradis isto ali gledas samo normalnu komponentu elektricnog polja koje potice od tackastog naelektrisanja pa se ta poslednja formula menja.
Citat:
c)odrediti ukupnu velicinu naelektrisanja indukovanog na povrsini ravni
Posto smo nasli povrsinsko naekeltrisanje za svaku tacku (x,y) onda samo treba da izracunas povrsinski integral gde x i y uzimaju vrednosti od minus beskonacno do plus beskonacno. Ti pokusaj ovo sve da ispises pa ako negde zapne vici
[Ovu poruku je menjao srki dana 04.02.2007. u 13:17 GMT+1]
Jedan zadatak iz elektrostatike
