[es] - Definicija realnih brojeva

uranium
Beograd

Član broj: 60097
Poruke: 543
*.eunet.yu.

Jabber: uranium@elitesecurity.org
ICQ: 324386953

+5 Profil

Re: Definicija realnih brojeva

^{10.10.2006. u 23:38 - pre 225 meseci}

@Farenhajt:

Ako prihvataš aksiomu izbora, taj žešće zeznut skup i te kako postoji

Dakle, postoji dobro uređenje realnih pa time i susedni elementi u smislu takvog uređenja

_{Attempt all the problems. Those you can do, don't do. Do the ones you cannot.}

Odgovor na temu

Farenhajt
Goran Kapetanović
Beograd

Član broj: 78132
Poruke: 449
62.193.129.*

+6 Profil

Re: Definicija realnih brojeva

^{11.10.2006. u 00:05 - pre 225 meseci}

Više sam pokušao da izvučem "zdravorazumski" ekstrakt iz postova galet@world-a nego što sam ulazio u to šta kad može, a kad ne može

Tačke susedne po dobrom uređenju skupa realnih brojeva neće, koliko vidim, biti i "vizuelno" (geometrijski) susedne (tj. susedne na način koji bi bio srodan "susednosti" u skupu prirodnih brojeva)... Ili možda grešim?... A čitava dilema i proističe iz "vizuelnog" tumačenja "realne" nule.

Odgovor na temu

uranium
Beograd

Član broj: 60097
Poruke: 543
*.eunet.yu.

Jabber: uranium@elitesecurity.org
ICQ: 324386953

+5 Profil

Re: Definicija realnih brojeva

^{11.10.2006. u 01:20 - pre 225 meseci}

@Farenhajt:

Niko ne zna kako bi to dobro uređenje izgledalo, jedino se zna da ono postoji (pod datim pretpostavkama) - ja sam to naveo jednim delom kao zanimljivost a drugim delom kao ilustraciju nečeg o čemu pokušavam da pričam već poslednjih

postova

Na primer euklidska geometrija ima razne modele a većina njih ne izgleda ni malo intuitivno - dakle pojam duži, linije...opisan nekim od standardnih sistema aksioma (i propratnim definicijama) uopšte ne mora da odgovara predstavi koju većina nas ima kada nam se pomene neki od tih pojmova.
Po pravilu, ključne stvari se ne dokazuju već se uzimaju kao aksiome, a u slučaju geometrije imamo dokazane mnoge lepe osobine odgovarajućeg sistema aksioma. Svako je slobodan da taj sistem preuredi po svom nahođenju ili izgradi potpuno novi i time (eventualno) dobije novu teoriju. Dakle, jedan od razloga zbog koga se ova rasprava toliko rasplinula je u tome što rečenice "Tačka ima delova" i "Tačka nema delova" same za sebe nemaju nikakvog matematičkog smisla. Matematički objekti nisu geografski objekti (ko je rek'o Slaviša B. Prešić?

) pa da možemo da kažemo nešto tipa: "Beograd se nalazi na ušću Save u Dunav".

Klasičan primer šta znači matematička naspram laičke interpretacije mat. pojmova je recimo geometrijska predstava jedinične sfere u zavisnosti od nametnute metrike. Odgovarajuće slike mogu se videti ovde a čik probaj nekog neupućenog da ubediš da su sve ono slike i dvodimenzionih sfera (tj. kružnih linija)

_{[Ovu poruku je menjao uranium dana 11.10.2006. u 03:02 GMT+1]}

_{Attempt all the problems. Those you can do, don't do. Do the ones you cannot.}

Odgovor na temu

Farenhajt
Goran Kapetanović
Beograd

Član broj: 78132
Poruke: 449
62.193.129.*

+6 Profil

Re: Definicija realnih brojeva

^{11.10.2006. u 09:52 - pre 225 meseci}

Sve je to u redu, ali opet - držim da je galet@world pošao od klasičnog, intuitivnog modela euklidske geometrije i došao do svega što je došao. I kao što si sam rekao, svako od nas može da sastavi sopstvenu aksiomatiku i da se njome silno ponosi. (Kao ilustraciju, uzmi naše dve aksiome u vezi s adicionim formulama

)

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.sr.gov.yu.

+2801 Profil

Re: Definicija realnih brojeva

^{13.10.2006. u 20:23 - pre 225 meseci}

Citat:

galet@world: O Nedeljkovim dobrim namerama najbolje govori on sam:

Citat:

Sa druge strane, ti mu ne možeš napisati udžbenik analize, pogotovu besplatno na ES.

Najzad da se oko nečega složimo. Ja zaista sam umem najbolje da govorim o svojim namerama. Takođe, stojim iza onoga što sam napisao. Zar zaista misliš da iko može da ti napiše udžbenik analize besplatno i da ti ga tek tako okači na internet? Možda i može ako je penzioner, ali uranium je tek student.

Uranium me je vrlo dobro razumeo. Cela ova rasprava je besciljna. On samo troši svoje dragoceno vreme pokušavajući da ti objasni realne brojeve, ali od tog posla (bar na ovaj način) nema ništa. Ti nećeš biti na dobitku, a on će biti na gubitku. Da bi ti razumeo zasnivanje realnih brojeva i matematičke analize (uključujući pojmove kao što su dužina, površina, zapremina i mera ugla), ne možeš proći "jeftinije" od 150 stranica teksta minimum, ako ne i više. Tako bi ti eventualno razumeo pomenutu tematiku. Zar zaista očekuješ od nekoga ko je student da ti napiše knjižurinu za dž i tek tako je okači na internet?

Ne kažem, postoje free softverski proizvodi koji su kvalitetni, pa i tekstovi koji su u sličnom duhu. No, u svakom slučaju, tako se nešto radi za malo širu publiku i postoje načini da se takvi projekti održe. Profesor Matematičkog fakulteta Dr Miodrag Mateljević je napisao za studente besplatne knjige u elektronskom obliku i okačio ih na internet. Svaka mu čast! No, on prima platu na fakultetu, pa mu se može. Ako neko nema druge izvore prihoda, onda mora nekako da reši problem finansiranja tog projekta. Postoje razni načini, ali nikako putem pisanja za jednu osobu za dž. Ne razumem šta tu nije jasno.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

galet@world

Član broj: 81985
Poruke: 1076
*.adsl.sezampro.yu.

+3 Profil

Re: Definicija realnih brojeva

^{25.10.2006. u 20:56 - pre 225 meseci}

Citat:

Nedeljko: Ne razumem šta tu nije jasno.

Dugo sam razmišljao da li da ti pomognem da razumeš ili ne.
Nisam izdržao da te držim u neizvesnosti i zato ovo moram da ti kažem:
Evo šta ti ne razumeš: Ako deliš jabuku na beskonačno mnogo delova - jedan takav deo je, ma koliki bio, deo jabuke!
Verujem da (ipak) razumeš šta sam ovim hteo da kažem.
Ja nisam hteo da se "ogrebem" za besplatan i problematičan udžbenik (koji je već mnogo puta napisan!), nego sam hteo da tebe besplatno nečemu naučim.
Ako ti neko uzme jabuku onda nemaš ništa od jabuke, jednako tako kao ni od onoga što nikad nisi ni imao.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.sr.gov.yu.

+2801 Profil

Re: Definicija realnih brojeva

^{27.10.2006. u 09:19 - pre 225 meseci}

Ama, kažem ja da ćemo uživati u tvojim časovima. Samo tako nastavi. No, ipak, da bi neko nešto preneo, prvo mora sam to da poseduje.

Citat:

galet@world: Ja nisam hteo da se "ogrebem" za besplatan i problematičan udžbenik (koji je već mnogo puta napisan!),

Da si ikada pročitao barem jedan u kome se zasnivaju realni brojevi, ne bi postavljao pitanja kao što je ono iz prvog posta ove teme. Uranijum ti je dobro odgovorio pitanjem - "A šta podrazumevaš pod količinom?", no ti ne možeš da shvatiš smislenost takvog odgovora.

Što se jabuke tiče, možemo umesto o njoj (koja nije matematički pojam) govoriti o skupovima tačaka (što jeste matematički pojam). Oni nisu isto što i realni brojevi, ali postoji veza izmežu skupova tačaka u prostoru i realnih brojeva. Ta veza se zove Lebegova mera koja (nekim, ne baš svim) skupovima tačaka u prostoru pridružuje realan broj ili beskonačnost (kao jedinstvenu konstantu). Prazan skup, tačka, prava i ravan svakako da nisu isto, ali u prostoru imaju istu Lebegovu meru - a to je 0. To je kao što crvena ruža i crveni karanfil nisu isto, ali imaju istu boju.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

galet@world

Član broj: 81985
Poruke: 1076
*.adsl.sezampro.yu.

+3 Profil

Re: Definicija realnih brojeva

^{27.10.2006. u 20:56 - pre 225 meseci}

Nedeljko

Drago mi je što te uveseljavam, kad već ne mogu da te naučim.
Ali da pokušam još jednom, pa ako ne uspem bar ću te nasmejati.
Ako imaš kilogram pšenice, onda tu pšenicu možeš da melješ iliti usitnjavaš koliko god hoćeš. Uvek od sitnog može biti sitnije.
Ali uvek ćeš imati kilogram brašna sve sitnijeg i finijeg.
“Brašno je neuništivo!!!”
(Nemoj misliti na atomske ili subatomske čestice, to je zamorno, nego zamisli da je brašno elementarna materija – tako će ti biti lakše)
I sad ako si podelio 1 kg pšenice na beskonačno mnogo delova dobio si onu tvoju nulu bez dimenzije, a kad bi pšenica bila moja - ja bi dobio nulu sa dimenzijom pšeničnog brašna.
Ti ne možeš da umesiš hleb od beskonačno mnogo tvojih nula, ja od mojih mogu.
Ja verovatno po tvom mišljenju opet grešim, pa verujem da ćeš se i na ovo moje brašno nasmejati!
Ali, nema veze, budi ti zdrav i veseo!

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.sr.gov.yu.

+2801 Profil

Re: Definicija realnih brojeva

^{28.10.2006. u 08:20 - pre 225 meseci}

Ajmo ovako, Imam 1kg gline. Podelim je na 1000 jednakih delova. Oni su mase po 1g. Dakle, svaki od njih ima pozitivnu masu. Te delove podelimo na po 1000 jednakih delova. Sada imamo 10⁶ delova (još uvek konačno mnogo) od kojih je svaki mase po 1mg. Podelimo svaki od njih na po 1000 jednakih delova. Sada imamo 10⁹ delova (ali ipak konačno mnogo) od kojih je svaki mase 1 mikrogram. Podelimo li i njih na po 1000 jednakih delova, imaćemo 10¹² delova (što je još uvek konačno mnogo) mase od po 1ng. I tako dalje, koliko god delili, uvek ćemo imati konačno mnogo delova. Podeli koliko god hoćeš konačno mnogo delova na po konačno mnogo delova, opet ćeš imati konačno mnogo.

E sad, Lebegova mera (na pravoj) skupa racionalnih brojeva (koji se sastoji od beskonačno mnogo tačaka) je 0, baš kao i od konačnih skupova tačaka uključujući i prazan skup. Lebegova mera (na pravoj) odsečka [0,1], (koji se takođe sastoji od beskonačno mnogo tačaka) je 1. Čak i u računu graničnih vrednosti (koji nema baš puno veze sa ovim) 0 puta beskonačno nije uvek nula, već u principu neodređen izraz. To znači da ako o jednom nizu znamo da teži nuli, a o drugom da teži beskonačnosti, to je i dalje nedovoljna količina informacija da bismo zaključili nešto o konvergenciji proizvoda tih nizova. Gde li si samo iskopao obrazac

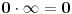
na koji se stalno pozivaš?

Da li znaš da je po teoremi Banaha i Tarskog moguće podeliti loptu na konačan broj delova (ne više od 11, a Robinson je broj delova smanjio na 5), tako da se od tih delova (samo kretanjem, bez ikakvih deformacija) mogu dobiti dve takve kugle? Jedna od posledica je da slona od deset tona možeš da podeliš na konačan broj delova i da ih nepromenjene sve smestiš u trbuh malog miša bez da se guraju.

http://mathworld.wolfram.com/Banach-TarskiParadox.html
http://en.wikipedia.org/wiki/Banach%E2%80%93Tarski_paradox
http://www.kuro5hin.org/story/2003/5/23/134430/275
http://www.math.hmc.edu/funfacts/ffiles/30001.1-3-8.shtml

Malo ozbiljniji tekst je

http://www.math.hmc.edu/~su/papers.dir/banachtarski.pdf

_{[Ovu poruku je menjao Nedeljko dana 28.10.2006. u 12:03 GMT+1]}

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

galet@world

Član broj: 81985
Poruke: 1076
*.adsl.sezampro.yu.

+3 Profil

Re: Definicija realnih brojeva

^{28.10.2006. u 18:18 - pre 225 meseci}

Ajmo i ovako:

Ako duzinu od 1 m podelis na 100 delova, pa opet svaki taj deo na 100 delova i t. d. svaki taj deo ima duzinu i dve krajnje tacke.
Pitanje je: kada taj deo prestaje da ima duzinu, odnosno kada prestaja da ima dve krajnje tacke?

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.sr.gov.yu.

+2801 Profil

Re: Definicija realnih brojeva

^{28.10.2006. u 19:04 - pre 225 meseci}

Odgovor: Ne prestaje nikad.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

galet@world

Član broj: 81985
Poruke: 1076
*.adsl.sezampro.yu.

+3 Profil

Re: Definicija realnih brojeva

^{29.10.2006. u 15:15 - pre 225 meseci}

Sad mi zaista vise nisi jasan - odgovorio si u skladu sa mojim misljenjem!

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.sr.gov.yu.

+2801 Profil

Re: Definicija realnih brojeva

^{29.10.2006. u 23:03 - pre 225 meseci}

Super. Znači, nema beskonačno kratkih duži koje se ne svode na tačku.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

galet@world

Član broj: 81985
Poruke: 1076
*.adsl.sezampro.yu.

+3 Profil

Re: Definicija realnih brojeva

^{30.10.2006. u 07:00 - pre 225 meseci}

Upotrebio si dve negacije, da ne bi doslo do zabune pitam - da li to znaci ca se svaka besonacno mala duzina svodi na tacku?

Odgovor na temu

chupcko
Negde
Beograd

Član broj: 5560
Poruke: 1141

Sajt: www.google.com

+63 Profil

Re: Definicija realnih brojeva

^{30.10.2006. u 10:17 - pre 225 meseci}

Jel se secate onog dokaza da je krodil duzi nego sto je siri ?

Lema 1: Krokodil je zeleniji nego sto je siri.
Dokaz:
Krokodil je zelen i po duzini i po sirini dok je sirok samo po sirini, pa je zato krokodil zeleniji nego sto je siri.
Kraj dokaza.

Lema 2: Krokodil je duzi nego sto je zeleniji.
Dokaz:
Krokodil je dugacak i sa gornje i donje strane, ali je zato zelen samo sa gornje, pa je zato krokodil duzi nego sto je zeleniji.
Kraj dokaza.

Dokaz sledi iz Leme 1 i Leme 2.

A sada malo ozbiljnosti: ajde bre kupi lepo analizu 1 i 2 od Adnadjevica i Kadelburga, ili neku drugi ekvivaletnu knjigu paaaaaaa ce sve biti jasnije :).

P.S. Tacka je ono ciji je deo nista :)))), prava je duzina bez sirine :)))))))

CHUPCKO

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.sr.gov.yu.

+2801 Profil

Re: Definicija realnih brojeva

^{30.10.2006. u 12:31 - pre 225 meseci}

@galetworld

Da, to znači to. Pod beskonačno kratkom duži tu podrazumevam duž koja je kraća od 1/n za svaki prirodan broj n. U standardnom zasnivanju polja realnih brojeva nema takvih pozitivnih veličina, pa je jedina preostala mogućnost 0. Tada se duž (ukoliko je zatvorena) svodi na tačku.

Citat:

chupcko: Jel se secate onog dokaza da je krodil duzi nego sto je siri ?

Krokodil svakako jeste više dugačak nego širok. Verovatno si mislio na dokaz da je obrnuto: širi je nego zeleniji zato što je zelen samo sa gornje, a širok i sa gornje i sa donje strane, a zeleniji je nego duži zato što je zelen i po širini i po dužini, a dugačak samo po dužini.

Citat:

chupcko: A sada malo ozbiljnosti: ajde bre kupi lepo analizu 1 i 2 od Adnadjevica i Kadelburga, ili neku drugi ekvivaletnu knjigu paaaaaaa ce sve biti jasnije :).

Ne vredi, džaba pričaš. Ja sam već omutaveo. On želi da samostalno ispituje koncept realnih brojeva, pri čemu ga ne zanimaju postojeći koncepti, već se oslanja na sopstvenu intuiciju o tome. Neka me ispravi ako grešim. No, pametnije je naučiti postojeće koncepte, pa im onda nalaziti nedostatke i razvijati nove koncepte koji ih otklanjaju.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

galet@world

Član broj: 81985
Poruke: 1076
*.adsl.sezampro.yu.

+3 Profil

Re: Definicija realnih brojeva

^{30.10.2006. u 17:48 - pre 225 meseci}

Citat:

Nedeljko: Pod beskonačno kratkom duži tu podrazumevam duž koja je kraća od 1/n za svaki prirodan broj n. U standardnom zasnivanju polja realnih brojeva nema takvih pozitivnih veličina, pa je jedina preostala mogućnost 0. Tada se duž (ukoliko je zatvorena) svodi na tačku.

Ta jedina preostala vrednost znači nepostojanje i prelaskom na tu vrednost učinio si kvalitativni skok koji ne pripada postupku deljenja, prešao si na nešto novo, drugo, nepostojeće koje nema nikakve veze sa onim što si započeo.
Rekao si da postupkom deljenja svaki deo ima dužinu i dve krajnje tačke i rekao si da taj deo ne prestaje nikad da ima dužinu i dve tačke ma koliko mali bio - i to je u redu, a sad kažeš da ipak prestaje i da se svodi na nulu.
Zašto? Zato što nam "preostaje" samo nula? Nula nije nikakva preostala mogućnost. Ona s tim ima veze isto toliko koliko i zeleni krokodil.
Nula o kojoj ti govoriš nikakve veze nema sa usitnjavanjem koje smo započeli. To je nešto drugo. Nešto što nije nastalo deljenjem dužine. Nešto što utrpavaš tamo gde ne pripada.
Duž se svodi na tačku!!! Fenomenalno.
Duž dakle nestaje. Uništena je. U jednom nedozvoljenom i besmislenom skoku! Alal vera matematičari.
Chupcko - ako me upućuješ na neke knjige onda me upućuješ i na autore tih knjiga - zato što ti lično ne ćeš da budeš autor razumnog odgovora. Šta su ti autori bolji od tebe, ako znaš odgovore.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.sr.gov.yu.

+2801 Profil

Re: Definicija realnih brojeva

^{30.10.2006. u 20:04 - pre 225 meseci}

Citat:

galet@world: Rekao si da postupkom deljenja svaki deo ima dužinu i dve krajnje tačke i rekao si da taj deo ne prestaje nikad da ima dužinu i dve tačke ma koliko mali bio - i to je u redu, a sad kažeš da ipak prestaje i da se svodi na nulu.

Nigde nisam rekao da u pomenutom postupku duži prestaju da imaju dužinu veću od nule. Napisao sam sledeće

Citat:

Nedeljko: Odgovor: Ne prestaje nikad.

Citat:

Nedeljko: Super. Znači, nema beskonačno kratkih duži koje se ne svode na tačku.

Citat:

Nedeljko: Da, to znači to. Pod beskonačno kratkom duži tu podrazumevam duž koja je kraća od 1/n za svaki prirodan broj n. U standardnom zasnivanju polja realnih brojeva nema takvih pozitivnih veličina, pa je jedina preostala mogućnost 0. Tada se duž (ukoliko je zatvorena) svodi na tačku.

Znači, to je bio opis pojma "beskonačno kratke duži" za koju sam tvrdio da je u postupku delenja nikada ne dobijamo.

Citat:

galet@world: Duž se svodi na tačku!!! Fenomenalno.

Vidiš, za razliku od tebe, ja vodim računa o tome da svi pojmovi budu precizno definisani, pa tako i ovde navodim definiciju duži koju koristim.

Za ma koje tačke A i B pod (zatvorenom) duži AB podrazumevam skup svih tačaka na pravoj AB koje su između tačaka A i B (ako ih ima) i još tačke A i B. U posebnom sličaju, ako je A=B, onda se duž AB svodi na jednu tačku.

Dakle, ja koristim tu definiciju. Možemo koristiti i neku drugu. To je stvar dogovora. Tu niko ne može biti "u pravu", niti "u krivu".

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

galet@world

Član broj: 81985
Poruke: 1076
*.adsl.sezampro.yu.

+3 Profil

Re: Definicija realnih brojeva

^{31.10.2006. u 07:28 - pre 225 meseci}

Citat:

Nedeljko: Znači, to je bio opis pojma "beskonačno kratke duži" za koju sam tvrdio da je u postupku delenja nikada ne dobijamo.

Duž koju ne dobijamo postupkom deljenja nije više duž.
"Duž" koja nema dva kraja nije više duž.
Beskonačno kratka duž je razmak između dve susedne tačke.
"Duž" koja se svodi na jednu tačku nije više duž - to je skok na drugu pojavu
Četvorougao kojemu nestane jedna strana nije više četvorougao nego trugao.
Ako vrh nekog trougla nije jedna tačka neko dve susedne onda je to još uvek četvorougao kojemu četvrtu stranu predstavlja beskonačno kratka duž.
Ako nestane ta beskonačno kratka duž t. j. ako u vrhu četvorougla ne postoje dve tačke nego jedna - onda je to skok na drugu pojavu - trougao.
Takva nula o kojoj ti govoriš znači nepostojanje, nemanje, isključenje, preskok na nešto drugo zbog nestanka nekog bitnog definišućeg elementa.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.sr.gov.yu.

+2801 Profil

Re: Definicija realnih brojeva

^{31.10.2006. u 08:29 - pre 225 meseci}

Citat:

galet@world: Duž koju ne dobijamo postupkom deljenja nije više duž.

Bravo! Znači, ako na realnoj pravoj deliš duž [0,1], onda [2,3] nije duž zato što nije dobijena postupkom delenja.

Citat:

galet@world: Beskonačno kratka duž je razmak između dve susedne tačke.

Ovo mi se još više sviđa. Znači, ako su A i B različite tačke realne prave (recimo da je Alevo od B), onda tačka (A+B)/2 može da ne pripada duži AB. Ako su P i Q "susedne tačke", šta je onda središte takve duži?

Citat:

galet@world: "Duž" koja se svodi na jednu tačku nije više duž - to je skok na drugu pojavu

Mogu da prihvatim takvu definiciju duži za nastavak razgovora. No, ona se ne može odnositi na moj post u kome sam koristio drugačiju terminologiju. Oko jezika se možemo dogoovriti. Sadržaj je bitan.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu