Mozda malo zadirem u offtopic, ali cisto ne mogu a da se ne umijesam:)..
Citat:
uranium:
Što se tiče zadatka sa dužinama - trik je u centralnoj projekciji:
.../cut/...
Na osnovu konstrukcije je jasno..
.../cut/...
S druge strane bilo koja tačka
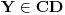
je slika tačno jedne tačke
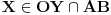
Jel se jos nekome cini ovakav nacin dokazivanja malo "manjkavim", ili sam to ja previse
paranoican?:)
Npr. pogledajmo zadnju, gore citiranu tvrdnju. Na osnovu cega zakljucujemo da je bilo koja tocka
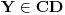
slika
tocno jedne tocke
?
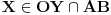
Ako je zbog toga sto smo prethodno rekli da se svaka tocka iz
preslika u razlicitu tocku iz
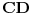
, kako znamo da su bas sve tocke iz
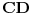
pogodjene ciljajuci zelenom zrakom kroz sve tocke iz
?
No cak i ta pretposljednja tvrdnja, u kojoj se tvrdi obrnuto, djeluje diskutabilno, jer se nekako previse oslanja na "ociglednost", a znamo da u matematici ne bi smjelo biti takvih zakljucaka.
Jer inace meni zadnja tvrdnja izgleda jednaka ovoj: bilo koja tocka
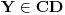
slika tocno jedne tocke
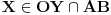
zato sto eto ja upravo kazem da je to tako :).
Volio bih vidjeti na sto se to tocno pozivamo kad napisemo tvrdnje poput tih?
(Napomena: posto prvi put ulazim u neku diskusiju, da jasno kazem kako mi nije namjera nista spocitati Uraniumu, dapace, volim citati njegove lijepe, leprsave i iscrpne odgovore :), te ovo pisem i pitam iz iskljucivo "matematickih" razloga)
Uglavnom, uvijek su me u slicnim dokazima smetale sintagme: "na osnovu konstrukcije zakljucujemo.." , "ocigledno je da.." i sl. Meni to izgleda nekako manjkavo, jer imam osjecaj da najcesce "zakljucujemo" ono sto nam pase da zakljucimo:).. Hocu reci, kako u tim dokazima nekako nedostaje matematicnosti tipa: na osnovu teorema tog i tog zakljucujemo to i to.
Evo da budem jasniji, galet@world je trazio rjesenje sljedeceg:
Citat:
galet@world:
Kažu da se pomoću bijekcije može dokazati da dve različite dužine imaju jednak broj tačaka.
Meni se svidja recimo ovakvo dokazivanje:
(vjerojatno postoji i mnogo koncizniji nacin, ali eto ja sam to sklopio nekako ovako: )
Uzmemo li da postoji jednoznacna korespodencija izmedju zatvorenih intervala iz skupa realnih brojeva i duzina na pravcu, problem se moze svesti na dokazivanje da su svaka dva zatvorena intervala ekvipotentna:
Uzmemo proizvoljni interval
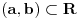
. Definiramo
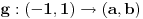
sa
.
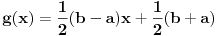
je bijekcija (lako se pokaze). To znaci da su
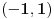
i
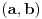
ekvipotentni
(dva skupa su ekvipotentna ako postoji bijekcija izmedju njih).
Kako je
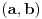
bio proizvoljan, to je dakle (-1,1) ekvipotentan i s bilo kojim
.
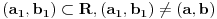
Kako je relacija "biti ekvipotentan" relacija ekvivalencije, to zbog njene simetricnosti i tranzitivnosti zakljucujemo da su bilo koja dva intervala
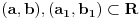
medjuosbno ekvipotentni.
Ovo je bio dokaz za otvorene intervale. Za prosirenje na zatvorene, trebamo pokazati da je proizvoljni (a,b) beskonacan skup, pa cemo se pozvati na teorem koji kaze da je
svaki beskonacan skup ekvipotentan uniji tog skupa i nekog konacnog skupa,
a taj konacni dodatak ce biti skup koji se sastoji od rubnih tocaka a i b, pa cemo dakle dobiti da je svaki (a,b) ekvipotentan s [a,b]. I na kraju primjenom simetricnosti i tranzitivnosti ekvipotentnosti, te uz vec dokazano za otvorene intervale, ustvrditi da su bilo koja dva dva zatvorena intervala ekvipotentna:
Pa pokazimo da je (a,b) beskonacan:
Imamo najprije:
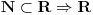
je beskonacan
(svaki nadskup beskonacnog skupa je beskonacan)
(a
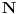
beskonacan jer udovoljava definiciji beskonacnosti:
skup X je beskonacan ako je ekvipotentan uniji tog skupa i skupa koji sadrzi element koji nije iz X. Npr. imamo da je
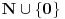
ekvipotentan skupu
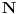
jer izmedju njih postoji bijekcija
. )
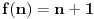
No
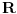
je ekvipotentan s (-1,1), jer postoji bijekcija izmedju njih:
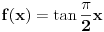
, dakle (-1,1) je takodjer beskonacan, a onda je takav i (a,b) jer smo prije ustvrdili da je ekvipotentan s (-1,1).
Dakle (a,b) je beskonacan.
Napravimo sad uniju
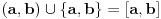
. To je unija beskonacnog i konacnog skupa, koja je, prema gore pomenutom teoremu, ekvipotentna skupu (a,b). Dakle [a,b] je ekvipotentan (a,b). Kako to vrijedi za proizvoljne a i b, to, visekratnom primjenom simetricnosti i tranzitivnosti relacije "biti ekvipotentan", slijedi da da su proizvoljna dva zatvorena intervala ekvipotentna.
Eto, ispade malo preopsirno, ali nadam se da je jasno sto sam htio pitati.. (ako nije, pogledajte recenice u prvom dijelu posta na cijim krajevima stoje upitnici :) )
[Ovu poruku je menjao Mlatko dana 22.09.2006. u 03:46 GMT+1]
while(sleeping) cat_wails(); wake_up(); for(int i=0;i<9;i++) shoot_cat(); rejoice();
goto(bed);
Re: Definicija realnih brojeva
Re: Definicija realnih brojeva
)
Re: Definicija realnih brojeva
Re: Definicija realnih brojeva
)
