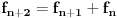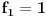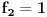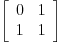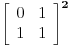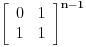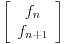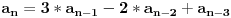Aha...znaci tebi nije jasno zasto i kako to radi?
Pa evo na prostom primeru ...
Znaci zelis da izracunas n-ti finonacijev broj....
Znamo da se fibonacijevi brojevi racunaju po formuli
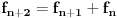
E takodje imamo prva dva clana finonacijevog niza a to su
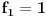
i
.
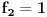
Sada zelimo da ta dva clana smestimo u jedan vektor tj. u matricu dimenzija 2 x 1. To bi izgledalo ovako:
Sada zelimo da napravimo neku matricu tako da ako je pomnozimo sa tim vektorom dobijemo sledeca dva clana fib. niza odnosno drugi i treci.
Ukoliko bi matricu
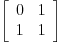
pomnozili sa prethodnim vektorom dobili bi upravo vektor sa drugim i trecim clanom, zato sto 0*1 + 1*1 = 1 nam daje drugi clan a 1*1 + 1*1 = 2 (primeti da je ovo upravo formula fibonacijevog niza) nam daje treci clan.
Znaci imamo
*
=
.
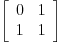
E sad ukoliko bi zeleli da dobijemo treci i cetvrti clan pomnozicemo matricu sa novodobijenim vektorom:
*
=
*
*
=
*
=
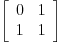
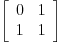
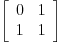
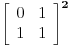
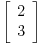
Sada je jasno da ako zelimo da dobijemo vektor sa
. i
. clanom trebamo samo da pocetnu matricu dignemo na
stepen i pomnozimo je sa pocetnim vektorom. Odnosno:
*
=
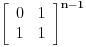
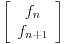
Poenta zadataka gde se ovo moze primeniti je da uocimo neku rekurentnu vezu koja mora biti homogena a zatim konstruisemo matricu mnozenja (upravo sam je tako nazvao:) ).
Recimo da je rekurentna formula koju smo uocili
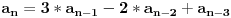
a pocetni vektor je
.
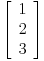
Matrica mnozenja bi izgledala ovako
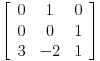
Nadam se da ti je ovo pomoglo
Don’t do drugs, sleep deprivation is better.
Primena matrica i operacija nad njima
