Re: Još jedan zadatak sa uglovimaHint: Polinom deobe kruga
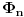na 
delova je nesvodljiv nad 
. Preko njega se lako nalazi minimalni polinom za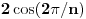 
.Naime, za
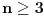je stepen polinoma 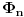paran broj 
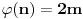. Lako se nalazi polinom 
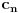takav da je 
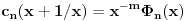.Za
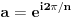važi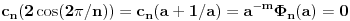 
. Polinom 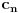je polinom sa racionalnim (čak celim) koeficijentima stepena 
. Dokažimo da je nesvodljiv nad .U suprotnom bi stepen broja
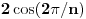nad poljem racionalnih brojeva bio 
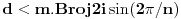je koren polinoma 
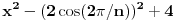, pa je nad poljem 
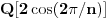stepena najviše 
, pa polje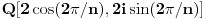 
koje sadrži 
predstavlja raširenje polja racionalnih brojeva stepena ne većeg od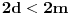 
, što je nemoguće jer je zbog nesvodljivosti polinoma 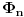nad poljem racionalnih brojeva stepen broja nad poljem racionalnih brojeva jednak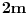 
.To nam omogućava računanje u polju
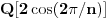. Pod tim podrazumevam operacije u polju nad brojevima izraženim u vidu linearnih kombinacija sa racionalnim stepenima brojeva 
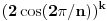za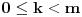 
. Zbir, razliku, proizvod i količnik brojeva u toj reprezentaciji možemo izračunati u istoj toj reprezentaciji. Zbog nesvodjivosti polinoma 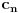, nula se može predstaviti na tačno jedan način, pa je na taj način dokaziv svaki tačan identitet u tom polju.Ako su svi uglovi na slici racionalni umnošci punog kruga, možemo izabrati
tako da ugao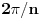 
bude najveći zajednički delilac uglova sa slike i pravog ugla. Tada je 
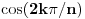izrazivo kao polinom (sa racionalnim, pa i celim koeficijentima) po 
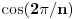. Takođe je 
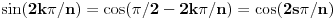za neko 
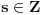.Onda račinamo koordinate tačaka sa slike u tom polju. Ako kraci nekog ugla imaju koeficijente pravaca
i 
, gde je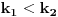 
, onda je prema formuli za razliku tangensa tangens tog ugla jednak 
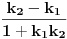.Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
