Državno takmičenje 2007, prvi zadatak za 4AZadatak:
Kod jednakokrakog trougla
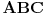je 
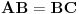i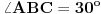 
. Tačka 
pripada stranici 
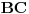trougla tako da je 
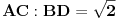. Izračunati ugao 
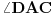.Rešenje 1:
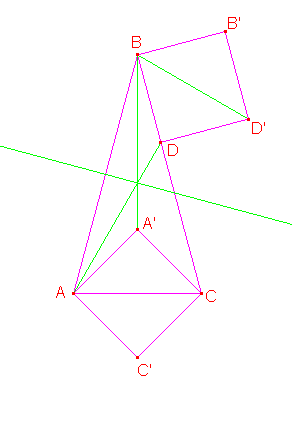
Docrtajmo kvadrate
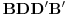i 
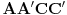. Primetimo da je 
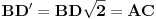i 
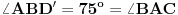. Prema tome, u odnosu na simetralu duži 
duž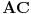 
preslikava se u 
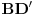, pa i kvadrat 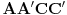u kvadrat 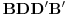. Dakle, 
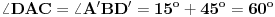.Rešenje 2:
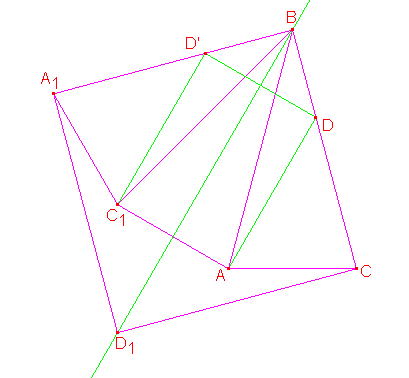
Uočimo tačke
i 
tako da su trouglovi 
i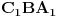 
podudarni s trouglom 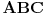, i neka je 
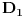četvrto teme kvadrata 
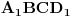. Takođe, neka je 
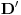tačka na 
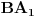takva da je 
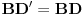. Primetimo da je 
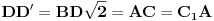, kao i da su duž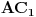i 
i 
normalne na pravu 
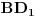, koja ih polovi. Prema tome, četvorougao 
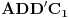je pravougaonik, pa je 
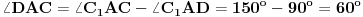.Rešenje 3:
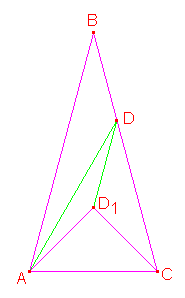
Neka je
tačka u unutrašnjosti trougla takva da je trougao 
jednakokrako-pravougli. Primetimo da je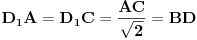 
. Kako je još i 
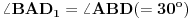, četvorougao 
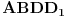je jednakokraki trapez. Prema tome, 
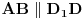, pa je 
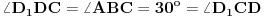, pa je 
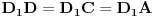. Dakle,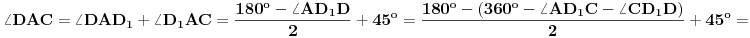 
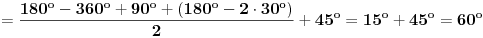.Rešenje 4:
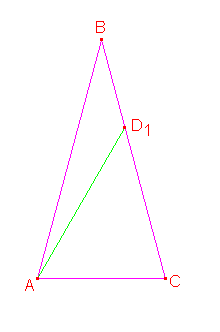
Uočimo tačku
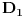na stranici takvu da je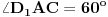 
. Primetimo da zbog sinusne teoreme važ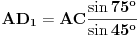i 
i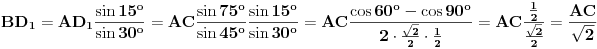 
. Pošto na stranici 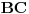postoji jedinstvena tačka za koju važi ovo važi, zaključujemo 
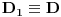, tj.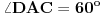 
.Rešenje 5:
Trigonometrijom se posle ne toliko dugog računa rešenje može dobiti potpuno pravolinijski. (Za ovo se, uzgred, odlučila velika većina takmičara.)
Rešenje 6:
Kompleksni brojevi takođe mogu da budu od pomoći, račun je opet pravolinijski i ne previše dugačak.
Ljubičice crvena, što si plava kô zelena trava.
