Teoreme su sortirane po mojoj proceni njihove složenosti.
1) Originalni oblik (1825)
Neka je dat trougao
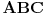 , i neka su konstruisani jednakostranični trouglovi
, i neka su konstruisani jednakostranični trouglovi 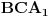 ,
, 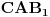 i
i 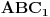 iste orijentacije. Obeležiimo sa
iste orijentacije. Obeležiimo sa 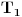 ,
, 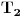 ,
, 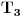 težišta trouglova
težišta trouglova 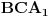 ,
, 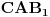 i
i 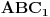 , redom. Tada je trougao
, redom. Tada je trougao 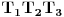 jednakostraničan (često se naziva i Napoleonov trougao — spoljašnji ili unutrašnji).
jednakostraničan (često se naziva i Napoleonov trougao — spoljašnji ili unutrašnji).2) Rigbijevo uopštenje Napoleonove teoreme (1991)
Džon F. Rigbi (John F. Rigby) je 1988. godine u časopisu Journal of Geometry br. 1-2 („Napoleon Revisited“, str. 129—146) dokazao sledeće uopštenje:
Neka je dat trougao
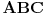 i neka su tačke
i neka su tačke 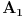 ,
, 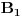 i
i 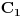 takve da su trouglovi
takve da su trouglovi 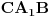 ,
, 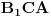 i
i 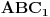 slični i iste orijentacije. Neka su
slični i iste orijentacije. Neka su 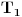 ,
, 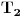 i
i 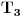 tri odgovarajuće tačke trouglova
tri odgovarajuće tačke trouglova 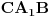 ,
, 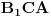 i
i 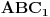 , redom. Tada je i trougao
, redom. Tada je i trougao 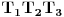 sličan sa trouglovima
sličan sa trouglovima 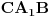 ,
, 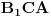 i
i 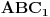 .
.Očigledno, ako su pomenuti trouglovi
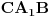 ,
, 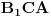 i
i 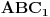 jednakostranični a tačke
jednakostranični a tačke 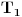 ,
, 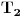 i
i 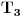 njihova težišta dobijamo tvrđenje 1).
njihova težišta dobijamo tvrđenje 1).3) Fukutina generalizacija Napoleonove teoreme (1997)
Džiro Fukuta (Jiro Fukuta) je 1996. u broju 69 časopisa Mathematics Magazine („Problem Proposal 1493“, str. 67) postavio sledeću hipotezu, koju je O. P. Losers (O. P. Lossers) dokazao i njegov dokaz objavljen je u narednom, 70. broju časopisa Mathematics Magazine 1997. godine („Solution to Problem Proposal 1493“, str. 70-73).
Neka je dat trougao
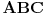 i neka tačke
i neka tačke 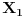 ,
, 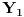 i
i 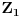 pripadaju stranicama
pripadaju stranicama 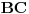 ,
, 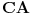 i
i  , redom, tako da je
, redom, tako da je 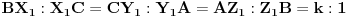 i neka tačke
i neka tačke 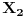 ,
, 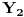 i
i 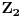 pripadaju stranicama
pripadaju stranicama 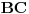 ,
, 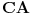 i
i  , redom, tako da je
, redom, tako da je 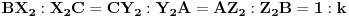 . Neka su
. Neka su 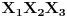 ,
, 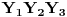 ,
, 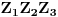 ,
, 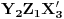 ,
, 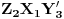 i
i 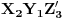 isto orijentisani jednakostranični trouglovi. Neka je
isto orijentisani jednakostranični trouglovi. Neka je 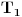 težište trougla
težište trougla 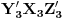 ,
, 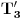 trougla
trougla 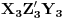 ,
, 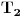 trougla
trougla 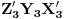 ,
,  ,
, 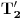 trougla
trougla 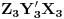 . Tada je šestougao
. Tada je šestougao 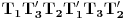 pravilan i njegov centar je u težištu trougla
pravilan i njegov centar je u težištu trougla 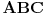 .
.Očigledno je da je trougao
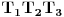 jednakostraničan, što će reći da u slučaju
jednakostraničan, što će reći da u slučaju 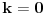 dobijamo tvrđenje 1).
dobijamo tvrđenje 1).4) Čerinovo uopštenje Fukutine generalizacije (1999)
Zvonko Čerin je 1999. godine u časopisu Radovi Matematički („Isocentroidal triangles and regular hexagons“, str. 227—239) dodatno uopštio tvrđenje 3).
Neka je dat trougao
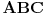 i neka tačke
i neka tačke 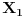 ,
, 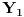 i
i 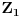 pripadaju stranicama
pripadaju stranicama 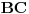 ,
, 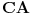 i
i  , redom, tako da je
, redom, tako da je 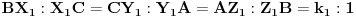 i neka tačke
i neka tačke 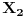 ,
, 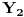 i
i 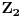 pripadaju stranicama
pripadaju stranicama 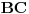 ,
, 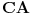 i
i  , redom, tako da je
, redom, tako da je 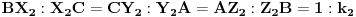 . Neka su
. Neka su 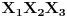 ,
, 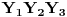 ,
, 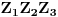 ,
, 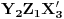 ,
, 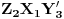 i
i 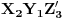 isto orijentisani jednakostranični trouglovi. Neka je
isto orijentisani jednakostranični trouglovi. Neka je 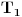 težište trougla
težište trougla 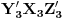 , T_3'[/tex] trogula
, T_3'[/tex] trogula 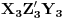 ,
, 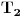 trougla
trougla 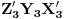 ,
,  ,
, 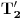 trougla
trougla 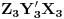 . Tada je šestougao
. Tada je šestougao 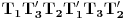 pravilan i njegov centar je u težištu trougla
pravilan i njegov centar je u težištu trougla 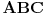 .
.Očigledno, u slučaju
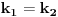 ovo se svodi na 3).
ovo se svodi na 3).5) Napoleon—Barlotijeva teorema (1940)
Džesi Daglas (Jesse Douglas) je u broju 19 časopisa Journal of Mathematics and Physics Masačusetskog tehnološkog univerziteta („Geometry of polygons in the complex plane“, str. 93—130) dokazao sledeće uopštenje teoreme 1):
Neka je dat affine-regular
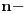 ugao (nisam siguran kako se prevodi ovaj izraz, to je mnogougao koji se može dobiti od pravilnog primenom affine transformacija, odnosno transformacija koje čuvaju kolinearnost i proporciju, u našem slučaju to je ma koja kompozicija translacije, rotacije, homotetije i iskošenja — shear). Ako su nad njegovim stranicama konstruisani pravilni
ugao (nisam siguran kako se prevodi ovaj izraz, to je mnogougao koji se može dobiti od pravilnog primenom affine transformacija, odnosno transformacija koje čuvaju kolinearnost i proporciju, u našem slučaju to je ma koja kompozicija translacije, rotacije, homotetije i iskošenja — shear). Ako su nad njegovim stranicama konstruisani pravilni 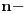 ugli iste vrste, onda njihova težišta formiraju pravilan
ugli iste vrste, onda njihova težišta formiraju pravilan 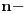 ugao. Ovde je verovatno potrebno dodatno pojašnjenje pojma „pravilni
ugao. Ovde je verovatno potrebno dodatno pojašnjenje pojma „pravilni 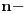 ugli iste vrste“. Naime, ovde pod pojmom „pravilan mnogougao“ nećemo podrazumevati samo konveksne figure već i zvezdaste, pa čak i degenerisane (tj. pretvorene u duž i sl.), za koje važi da su im sve stranice jednake i svi uglovi jednaki.
ugli iste vrste“. Naime, ovde pod pojmom „pravilan mnogougao“ nećemo podrazumevati samo konveksne figure već i zvezdaste, pa čak i degenerisane (tj. pretvorene u duž i sl.), za koje važi da su im sve stranice jednake i svi uglovi jednaki.Pošto je svaki trougao affine-regular, ovo je očigledno uopštenje teoreme 1).
Adrijano Barloti je (15 godina kasnije) u časopisu Bollettino della Unione Matematica Italiana br. 10 („Una proprietà degli
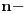 agoni che si ottengono transformando in una affinità un
agoni che si ottengono transformando in una affinità un 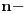 agono regolare“, str. 96—98) ponovo dokazao navedenu teoremu, i po njemu je dobila ime.
agono regolare“, str. 96—98) ponovo dokazao navedenu teoremu, i po njemu je dobila ime.6) Petr—Daglas—Nojmanova teorema (1905)
Karel Petr je 1905. u broju 34 časopisa Časopis pro pěstování matematiky a fyziky („O jedné větě pro mnohoúhelníky rovinné“, str. 166—172) dokazao sledeće tvrđenje:
Neka je u ravni dat
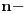 ugao. Nad njegovim stranicama konstruišemo pravilan
ugao. Nad njegovim stranicama konstruišemo pravilan 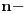 ugao određene vrste, zatim nad stranicama
ugao određene vrste, zatim nad stranicama 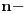 ugla koji se dobija spajanjem težišta konstruisanih pravilnih
ugla koji se dobija spajanjem težišta konstruisanih pravilnih 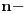 ugla konstruišemo pravilne
ugla konstruišemo pravilne 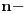 ugle neke druge vrste i postupak ponovimo
ugle neke druge vrste i postupak ponovimo 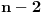 puta (postoji ukupno
puta (postoji ukupno  vrsta pravilnih mnogouglova i svaku od njih konstruišemo u po jednom koraku, na kraju nam preostane jedna koju nismo iskoristili). U tom slučaju težišta poslednjih konstruisanih mnogouglova formiraju pravilan mnogougao i to upravo preostale vrste.
vrsta pravilnih mnogouglova i svaku od njih konstruišemo u po jednom koraku, na kraju nam preostane jedna koju nismo iskoristili). U tom slučaju težišta poslednjih konstruisanih mnogouglova formiraju pravilan mnogougao i to upravo preostale vrste.Ovu teoremu su naknadno (nezavisno) dokazali i Džesi Daglas u već pomenutom radu, kao i Bernard Herman Nojman (Bernhard Hermann Neumann) u časopisu The Journal of the London Mathematical Society br. 16 („Some remarks on polygons“, str. 70—73). Njihovi radovi prošli su mnogo zapaženije nego prvobitan dokaz, pa se zbog toga u nazivu pominju sva tri imena.
Što se tiče ovih vrsta pravilnih mnogouglova evo i nekoliko primera pa će možda biti jasnije: postoje dva pravilna trougla — jednakostraničan pozitivno ili negativno orijentisan, zatim tri pravilna četvorougla — kvadrat pozitivno ili negativno orijentisan kao i degenerisan slučaj kada je
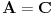 i
i 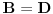 , zatim četiri pravilna petougla — konveksan i pentagram, oba mogu biti orijentisana pozitivno ili negativno, i tako dalje.
, zatim četiri pravilna petougla — konveksan i pentagram, oba mogu biti orijentisana pozitivno ili negativno, i tako dalje.Za
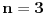 u konstruišemo tri jednakostranična trougla (u zavisnosti od vrste tj. orijentacije biće unutra ili spolja), i teorema nam kaže da njihova težišta formiraju jednakostraničan trougao (suprotne orijentacije od onih koje smo konstruisali, ali to je nebitno), iz čega sledi da i ovo zaista jeste uopštenje teoreme 1).
u konstruišemo tri jednakostranična trougla (u zavisnosti od vrste tj. orijentacije biće unutra ili spolja), i teorema nam kaže da njihova težišta formiraju jednakostraničan trougao (suprotne orijentacije od onih koje smo konstruisali, ali to je nebitno), iz čega sledi da i ovo zaista jeste uopštenje teoreme 1).Toliko od mene za sada, komentari, pitanja i sve ostalo su kao i uvek dobrodošli.
[Ovu poruku je menjao Bojan Basic dana 13.10.2006. u 22:31 GMT+1]




 Napoleonova teorema i njena uopštenja
Napoleonova teorema i njena uopštenja