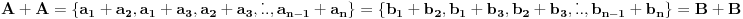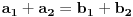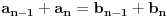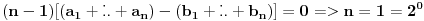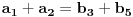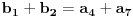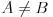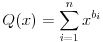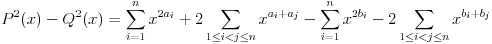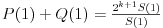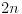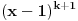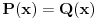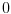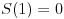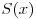Bojane, ja sam video da ti fale neka sitna obrazloženja i pojašnjenja, ali nisam reagovao misleći da će posetioci sami to kompletirati. No, kada već ima nejasnoća, hto bih da pojasnim ovo tvoje rešenje.
Prvo, ne vidi se gde si iskoristio uslov da su skupovi A i B različiti, bez koga tvrđrnje zadatka ne važi. Da kratiš nulom ne možeš, bez obzira da li je reč o polinomima ili brojevima. No, ti si ovde vršio skraćivanje polinomom
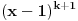
koji svakako nije nula polinom (nisu mu svi koeficijenti jednaki nuli), pa je skraćivanje dozvoljeno.
Sa druge strane, odakle ti pravo da deliš sa P(x)-Q(x)? Delenje nulom nije dozvoljeno, ali P(x)-Q(x) nije nula polinom jer su polinomi P(x) i Q(x) različiti budući da su skupovi A i B različiti.
Takođe treba obrazložiti zašto je zamena x sa 1 dozvoljena, jer u imeniocu imamo S(x). Šta ako je S(1)=0? Tada zmena ne bi bila moguća jer bismo dobili izraz oblika 0/0. Ako je k+1 višestrukost jedinice kao korena polinoma P(x)-Q(x), onda se on može napisati u obliku

za neki polinom S(x) kome 1 nije koren. Tada će biti S(1) različito od nule, pa je i ovaj korak dozvoljen.
Pritom je potpuno nebitno da li je P(1)-Q(1)=0 ili ne, jer sve prolazi bez obzira da li je pomenuta višestrukost jedinice u polinomu P(x)-Q(x) jednaka nuli ili je veća od nule. Svuda si umesto k+1 mogao da pišeš k. Uz ove dodatke je sve čisto.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

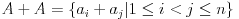 - ako se isti zbir pojavljuje više puta pišemo ga svaki put
- ako se isti zbir pojavljuje više puta pišemo ga svaki put i
i 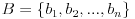 . Važi da je
. Važi da je 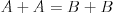 i
i 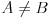 . Dokazati da je
. Dokazati da je 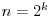 .
.



 Jedan zadatak sa fantastičnim rešenjem
Jedan zadatak sa fantastičnim rešenjem