• Naslovna
• FAQ
• Pravilnik
• O ES-u
• Tim
• Korisnici
• Statistike

 

• elitesecurity ::
• elitemadzone ::
• EMAIL ::
• RSS ::
• ES Mobile

  Niste ulogovani?  Username :   Password:   

• Registracija
• Zaboravili ste password?
• Flashback ▲▼
• Login problem?

 

Pretraga:

 

Srodne teme 23.06.2005. Mnogo lepa nejednakost 12.04.2006. cratanje grafa u matlabu s logaritamskom skalom 29.04.2006. Dokazati nejednakost 04.06.2006. Logaritamska struktura 26.08.2006. Nejednakost trougla 18.03.2007. logaritamska jednacina ???? 28.03.2008. Dokazati nejednakost 27.03.2009. Jedna nejednakost 11.08.2009. Jedan zanimljiv dokaz 13.07.2010. Logaritamska nejednacina_Za ispit_Help Navigacija Brisanje liste Aktuelne teme u ovom forumu: Još jedan zadatak sa uglovima Treći zadatak sa uglovima Ostala rešenja algebarske jednačine Lep zadatak sa uglovima Najmanje pozitivno realno r Ikosaedar i gustina ms matematika.... Jedan zadatak sa pravouglim trouglom Japanese | Can you solve this ? | Math.. Jednakostraničan trougao Logaritamska nejednakost Raspoređivanje slova Košarkaši lep zadatak Zanimljiv zadatak o uglovima trougla Stado Boga Sunca ... 2000 godina star .. Izaberite forum: Linux Linux aplikacije Linux desktop okruženja Linux hardware Windows desktop Windows aplikacije Zaštita Office Windows drajveri Office :: Word Office :: Excel Macintosh Mac hardware Mac software Iphone Enterprise Networking SOHO Networking Wireless Windows mreže Linux mreže Wireless :: WiMax Wireless :: Mikrotik Wireless :: Wireless oprema Linux/UNIX serveri i servisi Unix BSD Skript jezici Security Virtualizacija Cloud Computing Services Security :: Kriptografija i enkripcija .NET 3D programiranje Art of Programming Asembler C/C++ programiranje Kernel i OS programiranje Pascal / Delphi / Kylix Java Embedded sistemi Perl PHP Python Visual Basic 6 Veštačka inteligencija Security Coding XML GameDev - Razvoj Igara Ostali programski jezici PHP :: PHP za početnike PHP :: Smarty template engine .NET :: .NET Desktop razvoj .NET :: ASP.NET .NET :: WPF Programiranje C/C++ programiranje :: C/C++ za početnike Baze podataka MySQL Oracle Access MS SQL Firebird/Interbase PostgreSQL Fiksna telefonija VoIP Udruženje korisnika teleko.. GSM - telefoni GSM - upotreba GSM - servisiranje Mreže i novosti Smartphone Mreže i novosti :: Mobilni internet Mreže i novosti :: Telenor - korisnički servis Mreže i novosti :: VIP - korisnički servis Mreže i novosti :: MTS - korisnički servis Smartphone :: Symbian OS Smartphone :: Windows Mobile Smartphone :: Android GSM - telefoni :: Nokia PDA Uređaji GPS Portable Players Anonimnost i privatnost ISP Browseri E-mail Instant Messaging FTP Google Hosting ISP :: Wireless mreže i ISP ISP :: ADSL E-mail :: Anti-spam Instant Messaging :: IRC Hosting :: Domeni Google :: Gmail E-Marketing Web aplikacije Web dizajn i CSS Web dizajn softver Web razvoj Pretraživači i SEO Flash Javascript i AJAX Web dizajn i CSS :: Kritike Grafički dizajn Izdavaštvo 3D modelovanje Rasterska grafika Vektorska grafika 3D modelovanje :: CAD/CAM Matične ploče, procesori .. Video karte i monitori Storage Ostali hardver Overclocking & Modding PC Konfiguracije Laptopovi Vodič za kupovinu - PC har.. Tablet PC Muzička produkcija Audio kompresija Audio softver Video produkcija Video kompresija Video softver Multimedijalni uređaji Digitalni fotoaparati Digitalne kamere Home Theater Digitalni fotoaparati :: Fotografija Digitalni fotoaparati :: Vodič za kupovinu - Digita.. Elektronika Elektrotehnika Elektronika :: TV uređaji Elektronika :: Radio elektronika i tehnika Elektronika :: Mikrokontroleri Elektronika :: Audio-elektronika Auto-elektronika :: Tuning Vodič za učenje Vodič za posao Vodič za emigraciju Fizika Matematika Nauka Sertifikati Informatika Vodič za učenje :: Seminarski radovi Vodič za učenje :: Obrazovne institucije Vodič za emigraciju :: Život u USA Vodič za emigraciju :: Život u Norveškoj Vodič za emigraciju :: Život u Nemačkoj E-Poslovanje E-Kupovina IT pravo i politika razvoja IT događaji IT berza poslova IS i ERP Ekonomija Berza Cryptocoins IT berza poslova :: Arhiva IT berze poslova IT pravo i politika razvoja :: Registar Nacionalnog ID E-Poslovanje :: E-Transakcije E-Poslovanje :: Forex E-Kupovina :: Platne kartice Digitalna Televizija Advocacy Ankete Predlozi i pitanja Vesti Čekaonica Vesti :: ES leto manifestacija MadZone TechZone Poljoprivreda AutoZone MotoZone Svakodnevnica Video igre MadZone :: Zanimljivi linkovi MadZone :: Kultura TechZone :: Ergonomija TechZone :: Grejanje TechZone :: Klimatizacija TechZone :: Bela tehnika AutoZone :: Fiat Panda club Lista poslednjih: 16, 32, 64, 128 poruka.

miki069 Član broj: 161528 Poruke: 2056 109.245.227.* +390 Profil Re: Logaritamska nejednakost 23.01.2025. u 14:57 - pre 2 meseca Da li bi ceo dokaz mogao jednostavnije, uz predhodni dokaz, da je: log(9)*log(11) < 1 ? Taj dokaz znam da izvedem. Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.dynamic.isp.telekom.rs. +2801 Profil Re: Logaritamska nejednakost 23.01.2025. u 16:14 - pre 2 meseca Biramo sve veće i veće k dok ne dobijemo interval za vrednost sa jedne strane nule, odakle zaključujemo da li je vrednost pozitivna ili negativna. Dokaz za šta znaš da izvedeš? Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

miki069 Član broj: 161528 Poruke: 2056 109.245.227.* +390 Profil Re: Logaritamska nejednakost 23.01.2025. u 17:05 - pre 2 meseca Znam da izvedem dokaz da je: log(9)*log(11) < 1 Da li bi posle tog dokaza bio otvoren neki lakši put? Samo glasno razmišljam. Tvoje rešenje je OK, nego me zanima da li ima direktnije rešenje. Bez Numeričke analize. [Ovu poruku je menjao miki069 dana 23.01.2025. u 20:03 GMT+1] Odgovor na temu

jans Član broj: 218504 Poruke: 50 77.243.31.* +2 Profil Re: Logaritamska nejednakost 24.01.2025. u 23:23 - pre 2 meseca Pitanje za Mikija. Da li je druga nejednakost "tvoj" zadatak? Ako nije, možda je uz zadatak bilo i neko uputstvo za rešavanje, ili nagoveštaj da je zadatak moguće uraditi elementarno. Zadatak može da se reši i tako što se, u skupu realnih pozitivnih brojeva, reši nejednačina ( odgovarajuća jednačina se reši numerički ) . 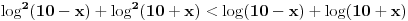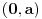Jedan interval skupa rešenja je , gde je . 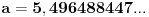Drugi interval koji sadrži brojeve suprotne brojevima iz prvog intervala, zbog simetrije izraza, ne daje nova rešenja. A pošto jedinica pripada navedenom intervalu, nejednakost je tačna, Odgovor na temu

miki069 Član broj: 161528 Poruke: 2056 109.245.227.* +390 Profil Re: Logaritamska nejednakost 25.01.2025. u 00:04 - pre 2 meseca Prva nejednakost je iz Krugove zbirke za II godinu. Rešenje u zbirci je isto kao prvo rešenje koje je dao kolega Jans. Drugo rešenje je mnogo elegantnije. Druga nejednakost nije iz zbirke. Sam sam je primetio dok sam pokušavao da rešim prvu. Odgovor na temu