Još jedan problem sa trouglomNeka je D središte hipotenuze AB pravouglog trougla
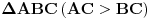. Ako su E i F preseci polupravih CA i CB, redom, sa pravom koja je u D normalna na CD, a tačka M središte duži EF, dokazati 
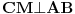.Moje rešenje (ili bar pokušaj):
Neka je
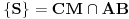. Posmatrajmo trouglove 
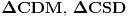i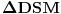 
. Neka je k opisani krug za trougao 
. Tada je prava MD tangenta na krug k u tački D, a duž SD tetiva kruga k. Ugao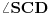 
je periferijski ugao nad tetivom SD. Poznato je da je ugao između tangente i tetive jednak periferijskom uglu nad tom tetivom, pa je 
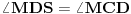. Zaključujemo da su trouglov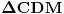i 
i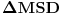 
slični, jer imaju dva podudarna ugla: 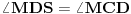i zajednički ugao 
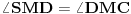. Zato i treći ugao mora da im bude podudaran: 
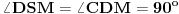. Dakle, 
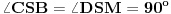, pa je 
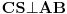, tj. 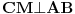.Međutim, ne bi važilo da je
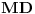tangenta na krug 
u tački 
da nije srediste od 
. Može li neko da mi kaže šta fali ovom dokazu i kako da bude ispravan...? Meni je to na slici izgledalo da je 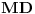tangenta, ali slika svakako nije dokaz. Ili ako neko vidi neko drugačije, jednostavnije rešenje. Ovo bi trebalo da bude zadatak za prvi srednje...Hvala unapred.
