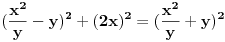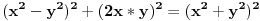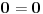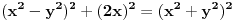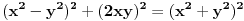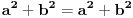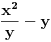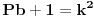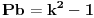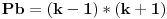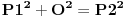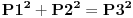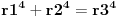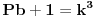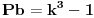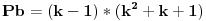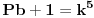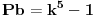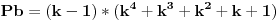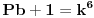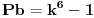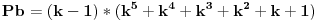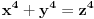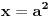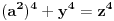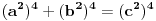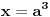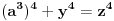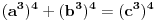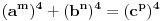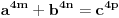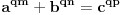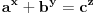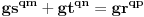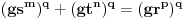@miki069,
Pb nije ista oznaka kao i P.
Pb je prost broj, a P je povrsina. mozda sam nedovoljno naglasio distinkciju pa je dovelo do nerazumevanja.
nego, evo jos jedne stvari.
imamo dokazano da je nemoguce
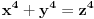
. drugim recima, za bilo koje celo x, ne postoje celi brojevi y i z za koje je formula tacna.
to je za stepen 4. ako hocemo dalje da ispitamo za stepen 8, onda napravimo zamenu
.
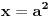
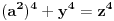
ali kako smo videli da y i z ne mogu biti celi brojevi a da je jednacina tacna, onda oni ne mogu biti ni stepeni celih brojeva. dakle,
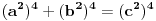
nije tacno.
ako sad uvedemo zamenu
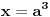
u prvu netacnu jednacinu dobijamo
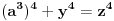
a kako, opet, y i z ne mogu biti celi brojevi, onda ne mogu biti ni stepeni celih brojeva, u konkretnom slucaju
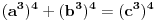
itd, za bilo koji stepen koji uzmemo.
kako y i z nisu celi brojevi, onda oni nece biti stepen nijednog broja.
uopsteno, to je
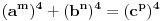
ili
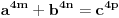
kako je fermatova dokazana za sve stepene a ne samo 4, onda je jos opstiji oblik jednacine
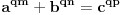
i ona je nemoguca.
ovo bi se moglo opisati: jednacina je nemoguca kada su osnove razliciti celi brojevi, a stepeni imaju jednog delioca koji je isti.
medjutim, evo opovrgavanja ovoga.
bilova hipoteza
http://en.wikipedia.org/wiki/Beal's_conjecture
tvrdi da je jednacina oblika
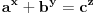
tacna kada osnove (a,b, i c) imaju jednog zajednickog delioca. ovo je i potvrdjeno racunarski do 1000 cini mi se za promenjive.
a to je suprotno zakljucku koji sam malopre napisao. jedina mogucnost je da gresim u izvodjenju, ali ne znam u kom delu?
celi brojevi u pt pomocu 2 promenjive
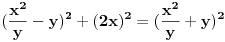gde je 
deljivo sa y, a i jedno i drugo (x i y) su celi brojevi. 
