Citat:
Ivan Dimkovic: Sampionstvo (tj. programiranje bez elementarnog znanja CS-a) obicno puca pri pisanju paralelnog koda ili koda koji zahteva preciznost (floating point domen). Tu se moze videti i najvise "genijalnosti" tipa poll-ovanje/busy-waiting, racing-kondicije,
neadekvatno tretiranje floating-point brojeva itd.
Ja sam šampionstvo po pitanju tretiranja floating point brojeva gledao na odbrani magistrature iz računarstva na Matematičkom fakultetu u Beogradu (da ne pljujem samo Elektrotehnički fakultet u Beogradu). Čovek je imao ulaz koji se sastoji od nekog broja realnih veličina, a izlaz mu je bio u konačnom skupu. Hteo je da nađe metodu koja izbegava poređenje s nulom, što je u takvim slučajevima nemoguće, jer ako su podskupovi od R
n koji odgovaraju tim izlazima otvoreni neprazni skupovi (tj. nema viška u skupu mogućih rezultata), a pokrivaju ceo R
n (uvek se dobija nekakav izlaz) i disjunktni su (jer se uvek dobija samo jedan izlaz), onda je R
n topološki nepovezan skup, što nije tačno (to je poznata teorema). To dalje znači da ne mogu svi ti skupovi biti otvoreni, pa postoji bar jedna kritična tačka u čijoj ma koiko maloj okolini ima tačaka iz raznih od tih skupova, tj. proizvoljno mala greška može proizvesti pogrešan zaključak, tj. mora se koristiti poređenje s nulom. Lik je napravio algoritam koji naravno sadrži poređenje s nulom (samo umotano u jednu lepu reč, tj. jedan matematički pojam, ali ga ima u računanju toga) i tako postigao cilj magistrature da se taj problem eliminiše. Rečeno je da toga nigde nema u literaturi. Pitam se samo zbog čega.
E, sad, ja tu ne bih svaljivao drvlje i kamenje na kandidata, jer svako može da se zaj
ebe, ali tu je bio mentor, pa toliki članovi komisije i da ga niko ne upozori prilikom izrade teze.
No, da pitam tebe Ivane kako se boriš sa tim problemom. Zamisli da su ti na ulazu dati realni brojevi
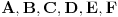
i da treba da na izlazu kažeš da li je skup tačaka u ravni Oxy dat jednačinom
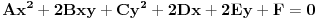
parabola ili nije. Za to je potrebno i dovoljno da je bar jedan od brojeva
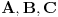
različit od nule, da je
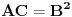
i da je
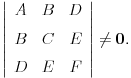
Recimo da treba odrediti da li je putanja komete parabolična ili nije.
Ili, evo još jednog problema. Realna funkcija realne promenljive je zadata deo po deo. Recimo,
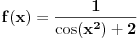
za
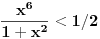
, odnosno
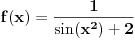
za
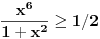
. Kako integraliti numerički tu funkciju npr. metodom pravougaonika? Poenta je da za dato

znaš koju formulu da koristiš za računanje

.
[Ovu poruku je menjao Nedeljko dana 19.12.2012. u 15:28 GMT+1]
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.