Istorija teorije relativnosti i razlozi njenog uvođenjaDa pođemo od Renea (Kartezijusa) Dekarta. Da bismo prirodne pojave mogli da izražavamo preko matematičkih funkcija vrlo je bitno da tačke prostorvremena predstavimo četvorkama realnih brojeva. Jednostavno, tako je mnogo lakše. To je Dekart uspešno uradio sa prostorom u geometriji, a slične ideje se mogu primeniti i na prostorvreme. Razlika je u tome što ćemo umesto trojki realnih brojeva imati četvorke od kojih su tru prostorne i jedna vremenska, pri čemu se prostorne sa jedne strane i vremenska sa druge, ne tretiraju baš na isti način.
Bijekcija (ili da li baš bijekcija ako naučnici kažu da vreme ima svoj početak, ali ostavimo to po strani) između prostorvremenskih tačaka i
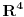se može uvesti na mnogo načina. Svaki od tih načina se zove koordinatni ili referentni sistem ili sistem referencije. Transformacije prelaska su transformacije kojima se ista tačka prostorvremena predstavljena kao četvorka jednog koordinatnog sistema transformiše u četvorku koja u drugom koordinatnom sistemu predstavlja istu tačku prostorvremena. Date su mi koordinate 
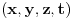nekog događaja u sistemu S i na osnovu njih treba da odredim koordinate 
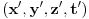istog događaja u sistemu S'.Veoma je važno praviti razliku između fizičkog događaja i fizičkog procesa. Fizički događaj je nešto što se desilo u jednoj tački (nema prostorno prostiranje) u jednom trenutku (nema vremensko prostiranje). Proces za razliku od toga može da traje i da se prostire.
U opštem slučaju, transformacije između dva sistema nisu ni nalik na linearne. Međutim, možemo se ograničiti na pravougle sisteme u kojima vreme ravnomerno protiče, koji su nešto mnogo određenije. Recimo, krut štap u njima neće menjati veličinu ako ga pomerimo sa jednog mesta na drugo ili ako ga zaokrenemo. Takođe, pojave za koje se očekuje približna ravnomernost u vremenu u takvim sistemima jesu takve.
Galileo Galilej je proučavao takve sisteme u međusobnom ravnomernom pravolinijskom kretanju. To znači da se svaka tačka koja miruje u jednom od tih sistema kreće ravnomerno i pravolinijski u drugom sistemu (sa istim vektorom brzine za sve tačke). Uočio je da se u tako povezanim sistemima pojave odvijaju na potpuno isti način, odakle je zaključio da osnovni prirodni zakoni imaju isti oblik u takvim sistemima. Taj princip se zove princip relativnosti. Ne znam za naziv, ali izgleda da sam princip potiče od Galileja. Galilej je pretpostavio najjednostaviji i najočigledniji oblik transformacija između takvih sistema (koje po njemu nose ime) i eksperimentalno ih proverio u uslovima i sa tačnošću koji su u to vreme bili mogući.
Ser Isak Njutn je to prihvatio i izgradio na takvim temeljima svoju teoriju. Jedan od Njutnovih zakona mehanike je zakon inercije, koji kaže da ako telo miruje i na njega ne deluje nikakva sila, ono ostaje da miruje, a ako se kretalo ravnomerno i pravolinijski i na njega ne deluje nikakva sila, ono nastavlja da se kreće ravnomerno i pravolinijski ne menjajući pravac smer i brzinu kretanja (kao i da ako na telo deluje neka sila, ono trpi ubrzanje jednako količniku sile koja deluje na telo i mase tela, ali taj deo nije relevantan za ovaj deo). Sistemi u kojima važi taj zakon se zovu inercijalni sistemi. Dokazuje se da ako taj princip važi u dva sistema, da oni moraju biti povezani linearnim transformacijama, kao i da ako važi u jednom sistemu, onda važi i u svakom drugom koji je sa njim povezan linearnim transformacijama.
Šta matematički znači princip relativnosti? Navedimo primer Njutnovog zakona gravitacije koji glasi da se materijalne tačke privlače silom koja je srazmerna proizvodu njihovih masa, a obrnuto srazmerna kvadratu njihovog rastojanja. Uz zakon inercije, odatle sledi da materijalna tačka sa istim početnim uslovima koji se odnose na položaj i bruinu u nekom trenutku pada u gravitacionom polju na isti način, bez obzira na bilo kakve svoje karakteristike, kao što je npr. masa. Drugim rečima, gravitaciono polje je polje ubrzanja, tj. svakoj tački prostorvremena se pridružuje neki vektor ubrzanja. Ono se može izraziti na sledeći način:
(1)
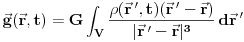,gde je
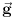vektor gravitacionog polja, 
gravitaciona konstanta, a 
funkcija gustine.Pređimo na neki drugi sistem koji je u ravnomernom pravolinijskom kretanju u odnosu na polazni u kome je zakon dat. Za to je potrebno da stare koordinate izrazimo preko novih. U klasičnoj mehanici su inercijalni sistemi povezeni Galilejevim transformacijama. Recimo da transformacija glasi:
, 
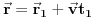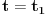
za neki konstantan vektor brzine
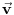. Ako to zamenimo u (1), dobijamo
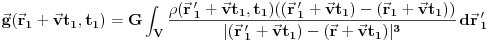.Ako je ovo izraz za
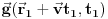, šta je izraz za 
?
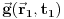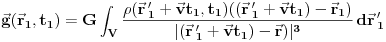.Posle jednostavne linearne smene u integralu (
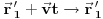), dobija se
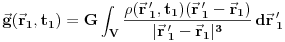,što znači da Njutnov zakon gravitacije ima isti oblik u oba sistema. Može se dokazati da je Njutnov zakon gravitacije invarijantan u odnosu na sve Galilejeve transformacije, a ne samo u odnosu na translatorno pomeranje. Napomenimo još da je za stransformisanje zakona bitno kako se koja (vektorska ili skalarna) veličina transformiše. Primera radi, u klasičnoj mehanici se vektori brzine i ubrzanja ne transformišu na isti način. Vektror brzine može promeniti intenzitet prilikom transformisanja, dok vektor ubrzanja ne može.
I tako je sve lepo išlo do XIX veka kada su otkrivene jednačine elektrodinamike, koje nisu invarijantne u odnosu na Galilejeve transformacije. Jedan od njihovih ekvivalenata su Jefimenkove jednačine iz kojih se neposredno vidi da se (po njima) elektromagnetno polje prostire brzinom svetlosti, a ne trenutno. Naime, na stanje u tački
u trenutku 
ne utiče stanje u tački 
u istom tom trenutku, nego u ranijem trenutku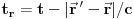 
, tj. taman toliko ranijem da bi signal brzine svetlosti ispaljen iz tačke 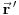u tom trenutku stigao u tačku 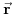u trenutku .Dakle, iz jednačina elektrodinamike sledi da se elektromagnetno polje prostire brznom svetlosti. Međutim, brzina nije apsolutan pojam. Na koji se sistem ona odnosi? Pa, na onaj u kome važe jednačine elektrodinamike u tom obliku. Obzirom da brzina svetlosti nije invarijantna u odnosu na Galilejeve transformacije, svetlost se u svim pravcima i smerovima može prostirati istom brzinom u samo jednom sistemu, pa samo u njemu mogu da važe jednačine elektrodinamike u tom obliku. Drugim rečima, ako bi postojao neki sistem u kome se svetlost prostire istom brzinom u svim pravcima i smerovima, odnosno u kojem važe jenačine elektrodinamike, nijedan sistem koji je sa njim je povezan Galilejevim transformacijama (nazovimo takve sisteme Galilejevim) i koji se kreće u odnosu na njega ne bi mogao da zadovoljava jednačine elektrodinamike u istom obliku, pa ako bi zakoni koji opisuju rad mernih instrumenata bili u ukupnosti invarijantni samo u odnosu na Galilejeve transformacije, taj privilegovani Galilejev sistem bi se mogao detektovati posmatranjem svetlosnih i elektromagnetnih pojava, što je u suprotnosti sa principom relativnosti. No, u to vreme se nije znalo za druge grupe transformacija, osim Galilejeve.
Odavde se nameće zaključak da se ne mogu istovremeno prihvatiti takva elektrodinamika, princip relativnosti i drugi zakoni koji su invarijantni samo u odnosu na Galilejeve transformacije, kao što su pomenuti Njutnov zakon inercije i Njutnov zakon gravitacije. Barem nešto od toga se mora žrtvovati.
Prvo se pokušalo sa "popravljanjem" jednačina elektrodinamike. No, nije išlo. Kada se brzina svetlosti zameni beskonačnošću u tim jednačinama, tj. odbace svi članovi koji se dele njome, dobijaju se jednačine koje jesu invarijantne u odnosu na Galilejeve transformacije, ali nisu u skladu sa izvršenim eksperimentima. Ono što fizičari XIX veka nisu znali, to je da se Maksvel-Hercove jednačine mogu malo manje osakatiti tako da budu invarijantne u odnosu na Galilejeve transformacije, a verovatno u skladu sa eksperimentima izvršenim u XIX veku. Dovoljno je zameniti u Jefimenkovim jednačinama brzinu svetlosti beskonačnošću samo u izrazu za
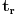, tj. zameniti 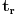sa . No, po takvim jednačinama (invarijantnim u odnosu na Galilejeve transformacije) se elektromagnetno polje prostire trenutno. Međutim, u drugoj polovini XX veka su u svemir ispaljivane razne sonde i brodovi (sputnjik i vojadžer) koje su sa bazom na Zemlji komunicirale putem elektromagnetnih talasa, čije je kašnjenje usled prostiranja brzinom svetlosti neposredno opaženo, tako da bi ta varijanta svakako otpala u XX veku.Zatim se pokušalo sa odbacivanjem principa relativnosti. Postavljena je bila čuvena hipoteza etra. Etar je nekakva sredina u odnosu na koju se svetlost i elektromagnetno polje prostiru istom brzinom u svim pravcima i smerovima. Ukoliko bi postojala takva globalna nepokretna sredina, onda Zemlja na svom putu oko Sunca ne bi mogla stalno da miruje u odnosu na etar jer joj je putanja kružna (dobro, ne baš tačno, ali je zatvorena). Ako bi Zemlja u nekom trenutku na putu oko Sunca mirovala u odnosu na etar, onda bi za pola godine (kada se nađe u suprotnoj tački svoje putanje oko Sunca) morala da se kreće brzinom 2v u odnosu na etar, gde je v brzina kojom Zemlja kruži oko Sunca (oko 30km/s).
Majklson i Morli su 1900 obavili čuveni eksperiment sa interferometrom u vezi s tim pokušavajući da izmere brzinu Zemlje u odnosu na etar. Brzina kruženja Zemlje oko Sunca je 0,0001c, tako da direktno merenje brzine svetlosti u raznim pravcima i smerovima sa tolikom tačnošću u to vreme nije bilo moguće. Stoga je bio osmišljen eksperiment u kome bi se detektovale male razlike u brzini svetlosti u raznim pravcima i smerovima za šta je po konstrukciji opreme bilo dovoljno da razlike u pređenom putu svetlosti unutar interferometra budu uporedive sa talasnom dužinom korišćene svetlosti (koja je jako mala), što je bilo sasvim dovoljno da se na korišćenom interferometru primeti da brzina svetlosti u svim pravcima i smerovima nije ista usled okretanja Zemlje oko Sunca. Kada su prvi put izvršili eksperiment, nikakve se promene nisu opazile. Kada se dobije neočekivan ishod eksperimenta, prvo se detaljno proverava sve, pa tek kada su eksperimentatori sigurni da nema nikakve greške, rezultat se prihvata kao činjenica. I tako su eksperimentatori nakon obavljenih provera pomislili da nisu imali sreće i da je Zemlja baš u tom trenutku na svom putu oko Sunca mirovala u odnosu na etar. Sačekali su neki broj meseci i koliko god da je puta ponovljen eksperiment, rezultat je bio isti - da nema nikakvih razlika u brzini prostiranja svetlosti u raznim pravcima i smerovima. Taj eksperiment je kao pokušaj merenja brzine Zemlje u odnosu na etar propao i uspešno je odbacio hipotezu o globalnom mirujućem etru.
Međutim, ostaje mogućnost da Zemlja svojom masom vuče za sobom neki lokalni etar i da je zato ishod Majklson-Morlijevog eksperimenta (za koji je kasnije Majklsonu dodeljena Nobelova nagrada za fiziku) bio takav. Međutim, ta mogućnost je odbačena na osnovu astronomskih posmatranja dvojnih zvezda (detalja se ne sećam).
Kada su propali pokušaji sa preformulacijom elektrodinamike i hipotezom etra, preostala je mogućnost odbacivanja Galilejevih transformacija. Lorencove transformacije su upravo izvedene jedine kao linearne transformacije koordinata u odnosu na koje su invarijantne Maksvel-Hercove jednačine elektrodinamike. Time su spaseni princip relativnosti i jednačine elektrodinamike po cenu revizije celokupne fizike (jer onda svi ostali zakoni moraju da se usklade sa Lorencovim transformacijama). Ta cena jeste vrlo visoka i upravo je to razlog što se nauka tome opirala dokle god je mogla, tj. to je razlog zbog kojeg je odbacivanje Galilejevih transformacija poslednje došlo na red, tj. tek kada su druge mogućnosti iscrpljene i otpale.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
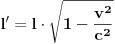
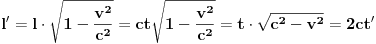
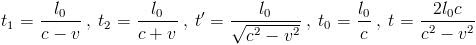, gdje je l0=ct0 dužina između prizme P i ogledala O.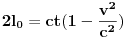
jedan od primjera pravilnijeg označavanja veličina (dosta dobro su opisani i ostali 