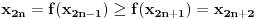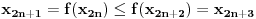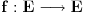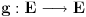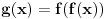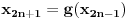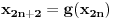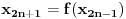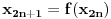Neka je
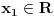 i
i  zadati niz realnih brojeva i neka je
zadati niz realnih brojeva i neka je  skup iz koga se reprodukuju clanovi niza. Onda imamo:
skup iz koga se reprodukuju clanovi niza. Onda imamo:1) Ako je f rastuca funkcija na E, niz
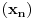 je monoton.
je monoton.2) Ako je f opadajuca funkcija na E, onda niz
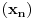 nije monoton, nego su njegovi podnizovi
nije monoton, nego su njegovi podnizovi  i
i 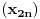 monotoni, i to u suprotnom smislu.
monotoni, i to u suprotnom smislu.Dokaz pod 1) je dat skoro detaljno i razumela sam ga, ali dokaz pod 2) nisam, jer pise:
Ako je npr.
 , onda je
, onda je 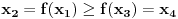 [to mi je jasno], zatim
[to mi je jasno], zatim  [i to mi je jasno], itd; dakle, indukcijom dobijamo da su
[i to mi je jasno], itd; dakle, indukcijom dobijamo da su  i
i 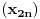 suprotni po monotonosti. Slicno se dobija i u slucaju da je
suprotni po monotonosti. Slicno se dobija i u slucaju da je 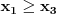 .
.Pokusavala sam to da dokazem indukcijom, ali ono sto meni nije jasno je sta mi je tu pretpostavka. Da li je moguce da se iz cinjenice da je
 i da f opada dokaze da je
i da f opada dokaze da je  rastuci niz? Ako kazem ovako:
rastuci niz? Ako kazem ovako:[BAZA]
 -- zadovoljeno, po pretpostavci
-- zadovoljeno, po pretpostavci[HIPOTEZA i KORAK] pretpostavimo:


i to se nikako ne slaze, jer bas treba da se dokaze da je
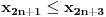 .
.Sta zapravo treba da dokazem? Da li prvo treba da dokazem da ako je f opadajuca, da
 npr. raste, a zatim da dokazem da
npr. raste, a zatim da dokazem da 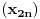 opada, pa obrnuto?
opada, pa obrnuto?




 Stav o monotonosti nizova
Stav o monotonosti nizova