1) Svaka ravnomerno neprekidna funkcija na nekom skupu je neprekidna na tom skupu. Obrat u opštem slučaju važi, ali postoji Kantorova teorema o ravnomernoj neprekidnosti po kojoj je svaka neprekidna funkcija na kompaktnom skupu ravnomerno neprekidna na njemu. Obzirom da je
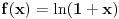
neprekidna funkcija na kompaktnom skupu
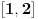
, ona je i ragvnomerno neprekidna na njemu. Primer neprekidne funkcije koja nije ravnomerno neprekidna je
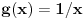
.
2) Ne znam da li se traži ispitivanje diferencijabilnosti po definiciji ili ne. Ako je odgovor negativan, izvod funkcije
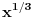
je funkcija
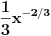
, koja nije definisana u nuli. Nediferencijabilnost u nuli se može dokazati po definiciji.
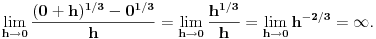
To si mogao da dobiješ na još jedan način: ako postoji konačan
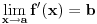
i funkcija

je neprekidna u tački

, onda je funkcija

diferencijabilna u tački

i ima izvod

, tj.
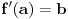
. Isto tako, ako je
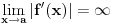
, onda
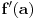
ne postoji. Ovo je neposredna posledica Lopitalovog pravila.
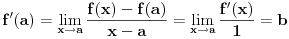
.
Što se diferencijabilnosti funkcija više promenljivih tiče, za diferencijabilnost funkcije u svakoj tački nekog otvorenog skupa dovoljno je da na tom otvorenom skupu postoje parcijalni izvodi te funkcije po svakoj od promenljivih i da su neprekidni na tom otvorenom skupu.
3) Primeni Rolovu teoremu.
4) Nije mi jasno šta je pitanje.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.