Evo jedan malo originalniji način, mada uz sličan početak.
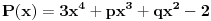
Da bi 1+i bila nula ovog polinoma onda i 1-i mora biti nula tog polinoma.
To znamo iz tvrđenja da ako je

koren polinoma sa realnim koeficijentima tada je i
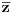
koren tog polinoma.
Dokaz je vrlo lak.
Ako je
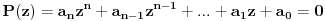
onda jasno mora da važi:
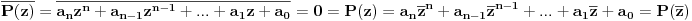
Pošto ovo važi tvrđenje sledi.
Polinom od kojeg smo pošli je četvrtog stepena. Možemo ga rastaviti na oblik
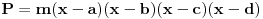
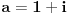
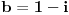
Otuda
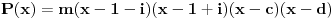
Pomnožimo prva dva člana:
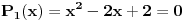
Pri tom važe Vietove veze:
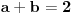
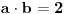
Poslednja dva:
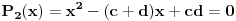
S obzirom da iz polazne jednačine sledi iz Vietovih veza:
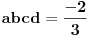
Odakle je:
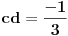
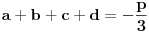
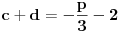
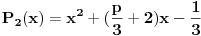
S obzirom da je:
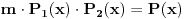
Da bi doveli do poklapanja koeficijenata uz
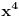
množimo to sa m=3.
Tako dobijamo da je
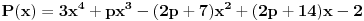
Da bi to bilo jednako polinomu
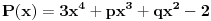
koeficijenti moraju biti isti.
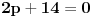
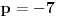
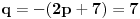
Lako se proverava da je rešenje jednačine
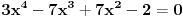
i
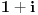
i
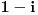
pa su dobijeni koeficijenti zaista rešenja.
[Ovu poruku je menjao Fermion dana 15.02.2011. u 10:09 GMT+1]