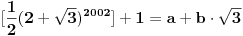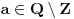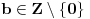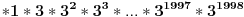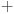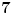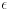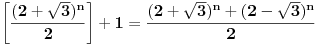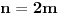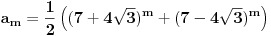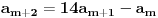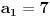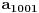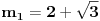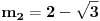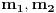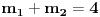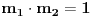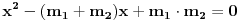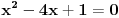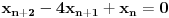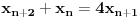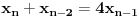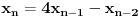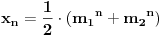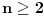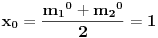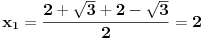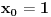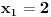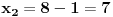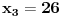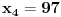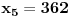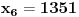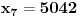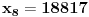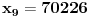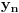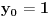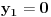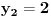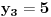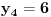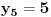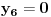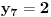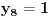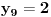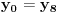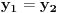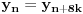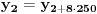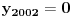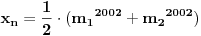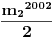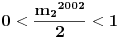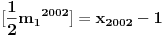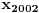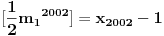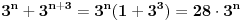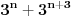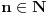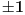Evo kako sam ja razumeo njihovo rešenje:
Označimo
,
.
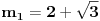
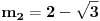
Nađimo kvadratnu jednačinu čija su rešenja
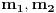
. Posto je:
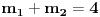
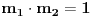
Iz Vietovih veza:
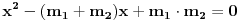
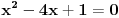
Ovo je karakteristični polinom za linearnu rekurentnu jednačinu:
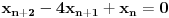
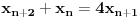
Pomeranjem indeksa:
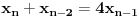
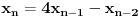
Rešenje ove jednačine je:
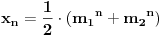
Sama rekurentna veza naravno ima smisla za
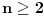
da ne bismo imali negativan indeks.
Za n=0 i n=1 izračunaćemo vrednost
prostom zamenom u rekurentnu vezu.
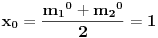
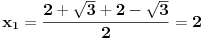
Koristeći vezu
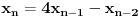
lako izračunavamo prve članove za
.
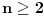
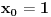
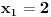
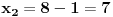
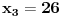
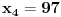
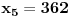
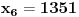
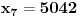
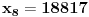
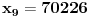
Ostatak pri deljenju broja
sa 7 obeležićemo sa
.
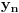
Ti ostaci iznose:
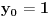
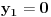
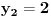
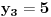
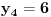
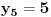
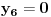
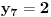
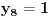
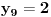
S obzirom da postoji ponavljanje članova, odnosno
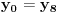
i
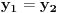
zaključujemo da je niz ostataka
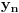
periodičan sa periodom 8.
To znači da je
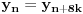
. S obzirom da je
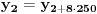
sledi da je
.
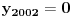
Posto je broj
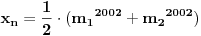
, a
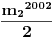
leži u intervalu
, tj.
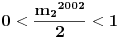
, sledi
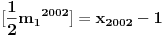
. Pošto je
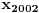
deljivo sa 7, sledi da je ostatak pri deljenju celog dela iz polaznog oblika jeste 6, ali pošto se na njega dodaje 1 dobija se oblik deljiv sa 7.
E sad, ja sam njihovo rešenje koje je stalo na 8 redova u knjizi, prilično interpretirao, pa je ispalo ovakvo dugačko, eventualne greške su sigurno moje :). Nisam koristio ni uvek iste oznake.
Ipak suština je u rekurentnim vezama i periodičnosti onih ostataka.
Zadatak sam inače našao knjizi "Uvod u teoriju brojeva", (sveska 15 iz "Materijala za mlade matematičare), na strani 9, zadatak 38, sa već pomenutog takmičenja, autori knjige su Vladimir Mićić, Zoran Kadelburg i Dušan Đukić.
Eto, pa ako imate neke ideje kako ovo da se uradi bez rekurentnih veza iznesite ih.
[Ovu poruku je menjao Fermion dana 07.01.2011. u 22:47 GMT+1]
[Ovu poruku je menjao Fermion dana 07.01.2011. u 23:23 GMT+1]
Zanimljiv zadatak iz teorije brojeva
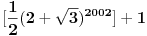deljiv sa 7.
.
