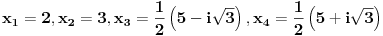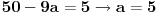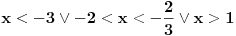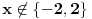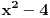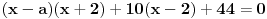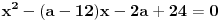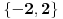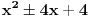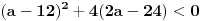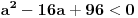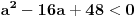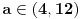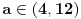[es] - Kvadratni problemi

Lucass

Član broj: 275549
Poruke: 4
*.cpe.vektor.net.

Profil

Kvadratni problemi

^{20.12.2010. u 21:20 - pre 174 meseci}

Ovo se resava preko t...

Ako ova funkcija sadrzi tacku A(3,5)

Ovde treba da se nadje za koje vrednosti parametra a izraz nema realna resenja... to je D < 0
D= b^2 - 4ac

Samo da se resi...

Zadaci su sa pismenog iz kvadratnih nejednacina i kvadratne funkcije... Krajnje lako, uradio sam sve, ali moram da isproveravam

Bio je jos jedan, ali je on tacan 100% Tako da...
Ako nekog ne mrzi da uradi... Bilo koji

Ja sam sve uradio, nego da proverim resenja. Hvala!

I da, meni nisu potrebni postupci, dovoljna su mi resenja

_{[Ovu poruku je menjao Lucass dana 20.12.2010. u 22:31 GMT+1]}

Odgovor na temu

atomant
Beograd

Član broj: 47540
Poruke: 263
*.dynamic.isp.telekom.rs.

+34 Profil

Re: Kvadratni problemi

^{20.12.2010. u 21:38 - pre 174 meseci}

2. Kada ubacis 3 u f(x) dobices

3. Mrzi me

4.

_{[Ovu poruku je menjao atomant dana 20.12.2010. u 23:08 GMT+1]}

If you can't explain it simply, you don't understand it well enough. A. Einstein

Odgovor na temu

Lucass

Član broj: 275549
Poruke: 4
*.cpe.vektor.net.

Profil

Re: Kvadratni problemi

^{20.12.2010. u 21:43 - pre 174 meseci}

Okej, hvala... Slazu mi se rezultati, svi sem ovog drugog... Tu se secam da sam dobio A 5... Bedak :(

Odgovor na temu

atomant
Beograd

Član broj: 47540
Poruke: 263
*.dynamic.isp.telekom.rs.

+34 Profil

Re: Kvadratni problemi

^{20.12.2010. u 22:09 - pre 174 meseci}

Pa i dobije se 5

If you can't explain it simply, you don't understand it well enough. A. Einstein

Odgovor na temu

Lucass

Član broj: 275549
Poruke: 4
*.cpe.vektor.net.

Profil

Re: Kvadratni problemi

^{20.12.2010. u 22:18 - pre 174 meseci}

Hah :D
Dobicu 4 onda svejedno, jer sam zeznuo cetvrti... Radio sam ga dobro, i sve, samo pogresno nacrtao grafik za jednu nejednacinu i ode sve :(

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.teletrader.com.

+2801 Profil

Re: Kvadratni problemi

^{21.12.2010. u 10:18 - pre 174 meseci}

Citat:

Lucass: Ovde treba da se nadje za koje vrednosti parametra a izraz nema realna resenja...

Jednačina je definisana za

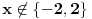
. Množenjem sa

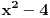
dobijamo ekvivalentan oblik

.

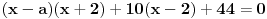
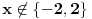
odnosno

.

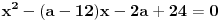
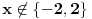
Ako je diskriminanta pozitivna, onda kvadratna jednačina ima dva realna rešenja, pa ako bar jedno od tih rešenja ne pripada skupu

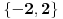
, polazna jednačina ima bar jedno realno rešenje. Znači, dobijena kvadratna jednačina se sme svoditi na jednačinu

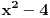
. Međutim, lako se proverava da to ne može biti slučaj.

Ukoliko je diskriminanta jednaka nuli, kvadratna jednačina ima jedno dvostruko rešenje, koje sme pripadati skupu

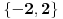
. Dakle, dobijena kvadratna jednačina se sme svoditi na jednačinu oblika

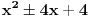
, ali se ispostavlja da ni to ne može biti slučaj.

Ako je diskriminanta negativna, onda kvadratna jednačina ne može imati realnih rešenja, pa ni polazna. Dakle,

,

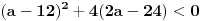
odnosno,

,

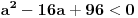
što je nemoguće. Dakle, polazna jednačina za ma koju vrednost parametra

ima bar jedno realno rešenje.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Lucass

Član broj: 275549
Poruke: 4
*.cpe.vektor.net.

Profil

Re: Kvadratni problemi

^{21.12.2010. u 20:05 - pre 174 meseci}

Ja sam tu koncano dobio da a pripada (4, 12) i tacno mi je... Dobio 5- :P Zbog ovog cetvrtog... No, nebitno, sad cu opet da uradim taj treci da vidim

Greska ti je u poslednjem koraku... Odakle ti +96? Tu je +48, onda se lepo resi :)

_{[Ovu poruku je menjao Lucass dana 21.12.2010. u 21:43 GMT+1]}

Odgovor na temu

atomant
Beograd

Član broj: 47540
Poruke: 263
*.dynamic.isp.telekom.rs.

+34 Profil

Re: Kvadratni problemi

^{21.12.2010. u 20:40 - pre 174 meseci}

Moram da se slozim sa Lucasom.

Nedeljko, nejednacina se svodi na:

I ona zaista ima resenja za

If you can't explain it simply, you don't understand it well enough. A. Einstein

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.teletrader.com.

+2801 Profil

Re: Kvadratni problemi

^{22.12.2010. u 08:24 - pre 174 meseci}

Da. Konačno rešenje je

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu