Radi se o tome da treba odrediti sve brojeve n takve da jednačina ima bar jedno rešenje u skupu racionalnih brojeva.
Jednačina je:
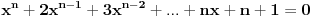
Trivijalno rešenje je n=1. Tada jednačina postaje x+2 = 0, i rešenje jeste racionalan broj.
Za n=2 uslov nije ispunjen, dalje je već teško proveravati... Verovatno bi matematička indukcija ovde mogla da bude put ka rešenju, ali voleo bih da nađem originalnije rešenje.
Ova polazna jednačina je simetrična i može se prikazati razbijanjem na grupe ovako:
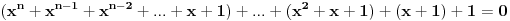
Prema tome članovi u ovakvim grupama obrazuju geometrijski niz čija se suma lako nalazi.
I kada se to što se dobije napiše malo pogodnije (imenilac x-1 je zajednički) dobije se još jedan geometrijski niz i suma jedinica u brojiocu pa se izraz još više pojednostavi.
Tako sam došao do sledećeg:
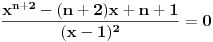
Pod uslovom da je x različito od 1 ova jednačina od koje sam krenuo može se napisati u znatno kraćem obliku:
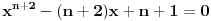
Zadatak je postao mnogo jednostavniji, pokušao sam da to još više uprostim, ali trenutno ne upevam ni to, ni da nađem rešenja polaznog zadatka.
Zato bih vas zamolio da mi pomognete da dovršim zadatak, a ako neko zna drugi način da ga reši, ili bar ima neku ideju, bio bih zahvalan da nju iznese.




 Zadatak sa određivanjem parametra n
Zadatak sa određivanjem parametra n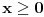
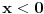

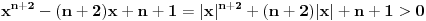
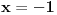
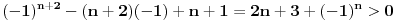
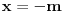
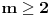
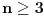
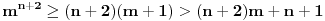


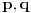
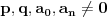
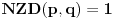

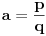
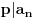
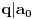
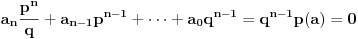
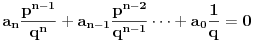

 Re: Zadatak sa određivanjem parametra n
Re: Zadatak sa određivanjem parametra n