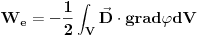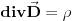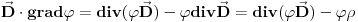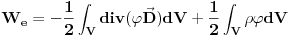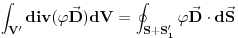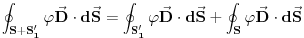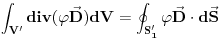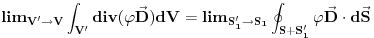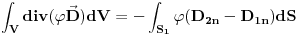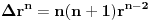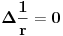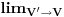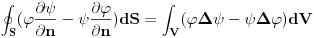[es] - Matematicki problem

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.dynamic.sbb.rs.

+33 Profil

^{11.09.2010. u 10:38 - pre 178 meseci}

- Grinova integralna teorema

Pretpostavimo da su potencijal i njegovi izvodi u celoj ovoj oblasti konacni i neprekidni izuzev na izvesnim povrsima

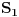, na kojima su nam dati skokovi potencijala i njegovih izvoda u pravcu normale.

Uzmimo da u Grinovoj integralnoj teoremi

oznacava potencijal ovog sistema, a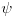

funkciju

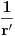, gde je

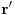rastojanje od tacke

u kojoj trazimo potencijal do proizvoljnog elementa zapremine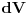

. Opkolimo povrsi

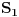zatvorenim povrsima

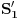, priljubljenim uz

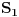, a tacku

sferom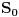

vrlo malog poluprecnika

. U oblasti izmedju ovih povrsi i povrsi

, koju oznacimo sa

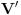potencijal i funkcija

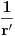su konacni i neprekidni, te na nju mozemo primeniti Grinovu teoremu: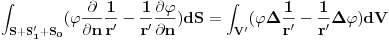

Kolko ja shvatam ovde je

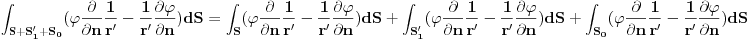
Prvi integral na desnoj strani otpada iz fizickih razloga i imamo

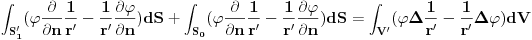
U svakoj tacki posmatrane oblast je

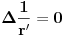. Zasto?.

Ako iskoristimo Poasonovu jednacinu elektrostatike

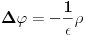, gde je

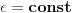, a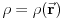

gustina slobodnih naelektrisanja imamo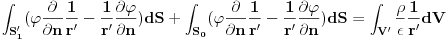

Kako sad izracunati integrale na levoj strani?

http://www.svijetfizike.com/

Prikačeni fajlovi

Grin.bmp - 576.05k

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.dynamic.sbb.rs.

+33 Profil

Re: Matematicki problem

^{11.09.2010. u 16:40 - pre 178 meseci}

Posto su slicni problemi u pitanju resih da nastavim u okviru ove teme.

Energija elektrostatickog polja je definisana kao

Znamo uslov

Postavlja se pitanje transformacije prvog integrala sa desne strane:

Potencijal i njegovi izvodi su svuda neprekidni osim na povrsima

- kao i u prvom postu!

je oblast na kojoj nemamo problema, pa na tu oblast primenimo Gausovu teoremu

Opet kolko ja shvatam u udzbeniku koji koristim

Drugi integral s desne strane otpadne iz fizickih razloga i dobijamo

Sada se koristi sledece

Zasto ovo vazi?

Odatle se dobija

Malo sam opotpunio problem ove teme. Problem je cisto matematicki. Voleo bih ako bi neko mogao da prokomentarise kolko je sve ovo korektno. U tekstu sam boldovao problematcne momente. Hvala svakom ko zeli da pomogne. Unapred hvala na odgovoru!

http://www.svijetfizike.com/

Prikačeni fajlovi

uz drugi post.bmp - 576.05k

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
212.200.65.*

+2801 Profil

Re: Matematicki problem

^{13.09.2010. u 07:30 - pre 177 meseci}

Citat:

petarm: U svakoj tacki posmatrane oblast je

. Zasto?.

To je ekvivalentno sa uslovom da je funkcija

harmonijska. Bez tog uslova to ne važi, tako da ovaj problem nije čisto matematički, već sigurno postoje fizički razlozi zašto je to harmonijska funkcija.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.uns.ac.rs.

+33 Profil

Re: Matematicki problem

^{22.09.2010. u 08:25 - pre 177 meseci}

Citat:

Nedeljko: To je ekvivalentno sa uslovom da je funkcija

harmonijska. Bez tog uslova to ne važi, tako da ovaj problem nije čisto matematički, već sigurno postoje fizički razlozi zašto je to harmonijska funkcija.

Da nisam proverio je li ova funkcija harmonijska, a dakako da jeste!

pa je

Citat:

petarm: Posto su slicni problemi u pitanju resih da nastavim u okviru ove teme.

Energija elektrostatickog polja je definisana kao

Znamo uslov

Postavlja se pitanje transformacije prvog integrala sa desne strane:

Potencijal i njegovi izvodi su svuda neprekidni osim na povrsima

- kao i u prvom postu!

je oblast na kojoj nemamo problema, pa na tu oblast primenimo Gausovu teoremu

Opet kolko ja shvatam u udzbeniku koji koristim

Drugi integral s desne strane otpadne iz fizickih razloga i dobijamo

Sada se koristi sledece

Zasto ovo vazi?

Odatle se dobija

Sta mislite o ovakvom resavanju ovih integrala i ima li smisla pustati

http://www.svijetfizike.com/

Odgovor na temu