Zordanova forma matriceZadatak:
Linearna transformacija A vektorskog prostora V u odnosu na bazu {e1,e2,e3} ima matricu:
A=
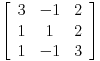
Naci Zordanovu formu matrice J matrice A, a zatim odrediti regularnu matricu P tako da je J=P-1AP
Rjesenje:
Ovako sam radila:
det (A-tI)=
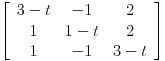=(3-t)(t-2)2Za t1=3 m=1 (sa m oznacavam visestrukost)
(A-t1I)=
=
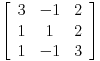
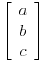-b+2c=0→c=2b
a-2b+2c=0
a-b=0→a=b
Et1={a,b,2b;a,bER}
dim Et1=2-----------------ovdje problem, naime kada nam je profesor govorio kaze da broj promjenjljivih kojima se izrazi baza je u stvari dimenzija (dim) te baze
Dalje
Za t2,3=2 m=2
(A-t1I)=
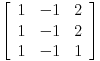
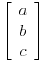=a-b+2c=0
a-b+2c=0
a-b+c=0
Prve dvije jednacine su iste, zbog toga odbacujemo jednu, pa imamo:
a-b+2c=0→a=b-2c
a-b+c=0
Et2={b-2c,b,c;b,c,bER}------------ovdje se pojavljuju dvije promjenljive to znaci:
dim Et2=2
Ne znam zbog cega mi je dimenzija jednaka visestrukosti nule svojstvene vrijednosti.
Takodje mislim da dimenzija kod visestruke nule svojstvene vrijednosti govori koliko imam Zordanovih blokova?
Dalje bi trebalo ici:
Wt2=Ker(A-tidv)2
to jest:
(A-t2I)2=(A-2I)2=
=
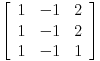
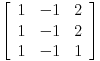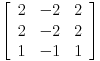
Zadatak jos nije gotov, ali me interesuju dimenzije i kako odredujemo koji je Zordanov blok, buduci da ih ima koliko ja znam 3 vrste, mozda grijesim. Unaprijed se svima zahvaljujem na pomoci.
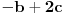
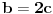
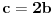
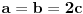
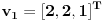
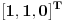
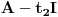
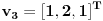
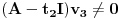
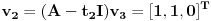
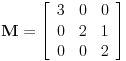
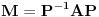
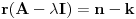
Re: Zordanova forma matrice