[es] - Kako izgleda učenje matematike čitanjem Vikipedije u slobodno vreme

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
212.200.65.*

+2801 Profil

Re: Kako izgleda učenje matematike čitanjem Vikipedije u slobodno vreme

^{17.07.2010. u 10:34 - pre 179 meseci}

Očigledno brkaš dve stvari:

1. Svi skupovi se mogu dobro urediti.
2. Neki skupovi se mogu dobro urediti.

1 važi u ZFC, a 2 već u ZF. Ja nigde nisam koristio činjenicu da se svi skupovi mogu dobro urediti, ali oni koji imaju alef, mogu u ZF.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

holononi

Član broj: 163572
Poruke: 658
*.adsl.verat.net.

+5 Profil

Re: Kako izgleda učenje matematike čitanjem Vikipedije u slobodno vreme

^{17.07.2010. u 15:41 - pre 179 meseci}

Opet si počeo da se baviš ličnostima i brkovima.

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
212.200.65.*

+2801 Profil

Re: Kako izgleda učenje matematike čitanjem Vikipedije u slobodno vreme

^{17.07.2010. u 22:48 - pre 179 meseci}

Kojim ličnostima? Za mene neko ko nema ime nije ličnost.

U nedostatku argumenata, davljenik se za slamku shvata.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

holononi

Član broj: 163572
Poruke: 658
*.adsl.verat.net.

+5 Profil

Re: Kako izgleda učenje matematike čitanjem Vikipedije u slobodno vreme

^{18.07.2010. u 09:41 - pre 179 meseci}

Na ovaj tvoj komentar primetiću samo da čovek treba biti nekulturan da bi tako nešto pisao.

Školski dokaz

:

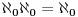
Neka je N₀ = N U {0} i F: N -> N₀ dato sa F(n) = n - 1, n element N. F je bijekcija i važi |N₀| = |N| =

Lema: Svaki broj n element N se može na jedinstven način prikazati u obliku:
n = 2^r(2s + 1), r, s element N₀. Označimo ovaj prikaz sa (*)

Postojanje prikaza se dokazuje indukcijom po n. Takodje se jedinstvenost lako dokazuje.

Definišemo preslikavanje f: N₀ x N₀ -> N sa

f((r,s)) = 2^r(2s + 1)

f je injekcija jer je prikaz (*) jedinstven. Da je f na sledi iz postojanja istog prikaza. Zato je f bijekcija odakle:

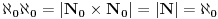
Ništa bez starog dobrog aksioma izbora.

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
212.200.65.*

+2801 Profil

Re: Kako izgleda učenje matematike čitanjem Vikipedije u slobodno vreme

^{18.07.2010. u 11:09 - pre 179 meseci}

I gde je tu aksioma izbora?

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

holononi

Član broj: 163572
Poruke: 658
*.adsl.verat.net.

+5 Profil

Re: Kako izgleda učenje matematike čitanjem Vikipedije u slobodno vreme

^{18.07.2010. u 11:20 - pre 179 meseci}

Funkcija izbora ako i samo ako aksioma izbora.

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
212.200.65.*

+2801 Profil

Re: Kako izgleda učenje matematike čitanjem Vikipedije u slobodno vreme

^{18.07.2010. u 12:16 - pre 179 meseci}

U kom konkretno koraku tvrdiš da si je upotrebio?

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

holononi

Član broj: 163572
Poruke: 658
*.adsl.verat.net.

+5 Profil

Re: Kako izgleda učenje matematike čitanjem Vikipedije u slobodno vreme

^{18.07.2010. u 13:23 - pre 179 meseci}

U drugoj jednakosti poslednjeg izvodnjenja. Mora se dokazati ekvipotentnost tih skupova.

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
95.180.8.*

+2801 Profil

Re: Kako izgleda učenje matematike čitanjem Vikipedije u slobodno vreme

^{18.07.2010. u 14:00 - pre 179 meseci}

Čeka, a čemu ti onda služi celo ono izvođenje ako tu ekvipotentnost treba ponovo da dokazuješ?

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

holononi

Član broj: 163572
Poruke: 658
*.adsl.verat.net.

+5 Profil

Re: Kako izgleda učenje matematike čitanjem Vikipedije u slobodno vreme

^{18.07.2010. u 15:57 - pre 179 meseci}

Ti se u svom dokazu pozivaš na multiplikativnu aksiomu (ekvivalent AC) (http://www.elitesecurity.org/t405228-0#2648386)

Ja sam samo pokazao da postoji funkcija izbora pa opet AC.

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
212.200.65.*

+2801 Profil

Re: Kako izgleda učenje matematike čitanjem Vikipedije u slobodno vreme

^{18.07.2010. u 16:23 - pre 179 meseci}

Ne, ja sam koristio TEOREMU ZF teorije da je

.

Sam si izveo tu jednakost sredstvima ZF, tako da nema potrebe da i ja navodim dokaz. Gde misliš da je u onom izvođenju korišćena AC?

Razumeš li o čemu pričam? Prvo si dokazao ekvipotentnost N x N i N, a onda na kraju tražiš da se opet dokazuje. Gde misliš da je AC u onom dokazu ekvipotentnosti?

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
212.200.65.*

+2801 Profil

Re: Kako izgleda učenje matematike čitanjem Vikipedije u slobodno vreme

^{18.07.2010. u 16:29 - pre 179 meseci}

Multiplikativna teorema tvrdi da u opštem slučaju, dakle za ma koji beskonačan skup A, važi da je A ekvipotentno sa A x A.

To tvrđenje je u nekim specijalnim slučajevima dokazivo sredstvima ZF.

Na primer, u ZF to tvrđenje važi za svaki beskonačan skup koji se može dobro urediti, tj. koji ima alef, a takođe za svaki sku A postoji njegov beskonačan nadskup B takav da je B x B ekvipotentno sa B. Toliko je dokazivo u ZF.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

holononi

Član broj: 163572
Poruke: 658
*.adsl.verat.net.

+5 Profil

Re: Kako izgleda učenje matematike čitanjem Vikipedije u slobodno vreme

^{18.07.2010. u 17:18 - pre 179 meseci}

Ti konstruišeš kule u oblacima. Neko će pomisliti da ja negiram kompletnu teoriju skupova. Iz toga što kažem da je 1+1 veće od jedan ne sledi da sam tvrdio da je veće od 5 kako otprilike izgledaju tvoji komentari i dokazi. Kao da niko osim tebe nije čuo za direktan proizvod. Ja ne galamim toliko pa sam samo diskretno napomenuo da je AC ekvivalent multiplikativnoj aksiomi. Iz toga si već trebao izvući zaključak da nema potrebe da objašnjavaš to što objašnjavaš jer neko će pomisliti da to nisu ekvivalentna tvrdjenja.

Dokaz koji sam naveo je ispravan (nije moj, možeš čuti na predavanjima). No kako je čovek konstruisao funkciju izbora izvukao sam zaključak da važi AC (opet ni taj stav nije moja umotvorina, dokaz imaš u literaturi). Možeš pobijati moj zaključak ali ne možeš tvrditi da ja tvrdim nešto što ne tvrdim.

Cabo
Lokanje u bircuzu

Član broj: 10942
Poruke: 684
*.vdial.verat.net.

+5 Profil

Re: Kako izgleda učenje matematike čitanjem Vikipedije u slobodno vreme

^{18.07.2010. u 18:40 - pre 179 meseci}

Ovaj, jel ovo još jedna od „onih“ tema u kojima neka reinkarnacija Tesle „ruši“ matematiku?

-______________________-

Kliknite da vidite kako da pišete matematičke formule u [tex]TeX[/tex]-u bez slanja slika

holononi

Član broj: 163572
Poruke: 658
*.adsl.verat.net.

+5 Profil

Re: Kako izgleda učenje matematike čitanjem Vikipedije u slobodno vreme

^{18.07.2010. u 18:57 - pre 179 meseci}

Ako imaš dokaz bez funkcije izbora slobodno ruši.

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
212.200.65.*

+2801 Profil

Re: Kako izgleda učenje matematike čitanjem Vikipedije u slobodno vreme

^{18.07.2010. u 19:35 - pre 179 meseci}

1. Gde si u onom dokazu našao izbornu funkciju?
2. AC nije nekakva dozvola za konstrukciju izborne funkcije, već postuliranje njenog postojanja u opštem slučaju, dakle, čak i onda kada ne možeš da je konstruišeš.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

holononi

Član broj: 163572
Poruke: 658
*.adsl.verat.net.

+5 Profil

Re: Kako izgleda učenje matematike čitanjem Vikipedije u slobodno vreme

^{18.07.2010. u 22:16 - pre 179 meseci}

Da li je moguće koristiti relaciju prirodnog uredjenja

na direktnom proizvodu skupova prirodnih brojeva ?

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
212.200.65.*

+2801 Profil

Re: Kako izgleda učenje matematike čitanjem Vikipedije u slobodno vreme

^{18.07.2010. u 22:18 - pre 179 meseci}

Misliš da su x,y i z uređeni parovi prirodnih brojeva?

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

holononi

Član broj: 163572
Poruke: 658
*.adsl.verat.net.

+5 Profil

Re: Kako izgleda učenje matematike čitanjem Vikipedije u slobodno vreme

^{18.07.2010. u 22:40 - pre 179 meseci}

Da si napisao "moguće je dokazati bez eksplicitnog pozivanja na AC" bilo bi ispravno jer zaista je moguć takav dokaz. Ti si napisao "važi u ZF" (i to čini mi se više puta). Ali taj dokaz implicira AC pa je tačno "važi u ZFC". To što ti izvrdavaš ne možeš izvrdati jer na direktnom proizvodu ne pomaže prirodno uredjenje.

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
212.200.65.*

+2801 Profil

Re: Kako izgleda učenje matematike čitanjem Vikipedije u slobodno vreme

^{18.07.2010. u 23:00 - pre 179 meseci}

Koji bre dokaz implicira AC? O čemu ti pričaš?

Na N x N postoji dobro uređenje, npr. leksikografski poredak.

Čovek te lepo pita gde ti je u onom dokazu AC, a ti stalno nešto vrdaš.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.