Srodne teme

14.04.2024. Re: Gde je Kejt? (samo pogrešni odgovori)
25.08.2007. Matematicki dokaz da je zena zlo
07.04.2006. Mordell-ova jednacina
19.03.2007. Nemoguci zadatak za 2 srednje elektrotehnicke
25.03.2007. Kako da vrednost iz nekog elementa u formi ostane..
06.06.2007. Hitno - Dva zadatka za maturski
30.06.2008. Trigonometrija,jos malo i gotovo ;)
23.02.2008. Recordi problem!??
03.04.2009. Izvodi, par opstih pitanja
05.04.2009. x+1=y-1 koliko je x, a koliko y

Navigacija

Brisanje liste

Lista poslednjih: 16, 32, 64, 128 poruka.

Koeficient k u trigonometrijskoj jednacini

[es] :: Matematika :: Koeficient k u trigonometrijskoj jednacini

Strane: 1 2 3

[ Pregleda: 14366 | Odgovora: 47 ] > FB > Twit

Autor

honijat

Član broj: 231185
Poruke: 40
*.ptt.rs.

Profil

Koeficient k u trigonometrijskoj jednacini

^{27.09.2009. u 13:51 - pre 177 meseci}

Ja imam jedan problem pri resavanju trigonometrijskih jednacina i recimo dobije se rezultat na pr :

x=pi/3+2kpi ili x=pi/4+kpi i slicno nije mi potpuno jasno sta predstavlja koeficient k.

Ako ima neko raspolozen da mi precizno objasni sta bukvalno predstavlja koeficient k ?

Odgovor na temu

enter08
student
MNE

Član broj: 200818
Poruke: 12
78.155.35.*

Sajt: www.enter08.com

Profil

Re: Koeficient k u trigonometrijskoj jednacini

^{27.09.2009. u 14:02 - pre 177 meseci}

Ako se ne varam to mozes zakljuciti posmatrajuci trigonometrijski krug. 2kpi znaci ce ugao biti uvijek djeljiv sa 90... Tj. za svako k 2kpi ce imati vrijednost 1 ili -1. I vrijednost cosinusa ce uvijek biti 0 s obzirom da je cos projekcija na x osu. Davno sam ovo ucio... Ne sjecam se vise.

Odgovor na temu

marko1981
Marko Nikolic
Beograd

Član broj: 123059
Poruke: 144
*.ptt.rs.

Profil

Re: Koeficient k u trigonometrijskoj jednacini

^{27.09.2009. u 15:06 - pre 177 meseci}

Uz rešenje

x=pi/3+2kpi

treba napisati za koje vrednosti k važi rešenje. K uglavnom pripada celom skupu celih brojeva (..., -2, -1, 0, -1, -2, ...).

To znači da rešenja ima bezbroj, odnosno da svaki broj x od sledećih, predstavlja rešenje jednačine:

...
x = pi/3 + 2*(-1)*pi = -5pi/3,
x = pi/3 + 2*0*pi = pi/3,
x = pi/3 + 2*1*pi = 7pi/3
...

A uzrok je periodicnost trigonometrijskih funkcija sa periodom 2pi, odnosno zbog toga što je:

sin(-5pi/3) = sin(pi/3) = sin(7pi/3) = ...

Naravno, da bi ovo shvatio, moraš i da razumeš trigonometrijski krug, kao što je napisao enter08.

Slično, rešenje jednačine sinx = 0 bi bilo

x = kpi, k e Z

jer je (sad ću napisati u stepenima, a ne u radijanima)

sin 0 = sin 180 = sin 360 = sin 540 = ... = 0

Odgovor na temu

honijat

Član broj: 231185
Poruke: 40
*.ptt.rs.

Profil

Re: Koeficient k u trigonometrijskoj jednacini

^{27.09.2009. u 20:09 - pre 177 meseci}

Ma slazem se ja sa svim tim i mislim da dobro razumem trigonometrijsku kruznicu . Ali koji su to uslovi zadatka kada ja mogu ili moram da uvrstim umesto k neki ceo broj i ako to uradim dali je u tom momentu tacno definisan ugao i nema mogucnosti za druga resenj.

_{[Ovu poruku je menjao honijat dana 28.09.2009. u 13:15 GMT+1]}

Odgovor na temu

EArthquake

Član broj: 20684
Poruke: 884
*.adsl.eunet.rs.

+67 Profil

Re: Koeficient k u trigonometrijskoj jednacini

^{27.09.2009. u 21:35 - pre 177 meseci}

pa ne moras uvek da preciziras koje je k tacno , samo stavis k pripada Z (k e Z :) )
sto oznacava da je skup resenja beskonacan , posto je sin/cos periodicna funkcija , kako su vec rekli ljudi u prethodnoh poruci

a obicno , kad ti treba konkretan ugao , uzimas k=0 ,

ili , ako ti je bas u datom zadatku iz nekog razloga lakse , neko drugo k

uslov zadatka recimo moze biti da ti se resenje nalazi izmedju 0 i 2pi
ili tako nesto , sto ti ogranicava interval

recimo , ako ti po uslovu zadatka resenje lezi u prvom kvadrantu
a ti dobijes resenje kao
pi/3 + 2*k*pi , onda uzimas samo pi/3 kao resenje

Odgovor na temu

honijat

Član broj: 231185
Poruke: 40
*.ptt.rs.

Profil

Re: Koeficient k u trigonometrijskoj jednacini

^{27.09.2009. u 23:10 - pre 177 meseci}

Pa i ne mislim ja da uvek treba precizirati ali predpostavimo da mi nesto ogranicava,neki vanredan slucaj na primer : imamo proizvodnju spiralnih opruga i da masini treba zadati uslov iz kog ugla pocinje da se savija zica i gde treba da bude kraj zici , i da to zapisemo ovako pocinje da savija iz pi/3 i da odseca zicu na 1080 stepeni od pocetne tacke. Alida to ne pisemo tako nego jednostavno pi/3+2*pi*3 ==> pi/3+6*pi . I koji je to uslov koji mi govori kada pisem 2*k*pi a kada k*pi ?

_{[Ovu poruku je menjao honijat dana 28.09.2009. u 13:36 GMT+1]}

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2154
*.broadband.blic.net.

+196 Profil

Re: Koeficient k u trigonometrijskoj jednacini

^{28.09.2009. u 17:39 - pre 177 meseci}

Citat:

honijat: . I koji je to uslov koji mi govori kada pisem 2*k*pi a kada k*pi ?

Na donjoj slici imaš periodičnu funkciju (crveno) sa periodom sedam.
I našao si presječnu tačku M sa onim plavim pravcem.Ali to nije jedino rješenje jer imamo još tih presjeka.
Neka je osnovno rješenje x(0)=4.Pokušaj napisati i sva ostala rješenja.
(Nije lijepo da pišeš nešto ovako:-3,4,11,18,...)

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Prikačeni fajlovi

P.fun..GIF

P.fun..GIF - 3.34k

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2154
*.broadband.blic.net.

+196 Profil

Re: Koeficient k u trigonometrijskoj jednacini

^{28.09.2009. u 23:43 - pre 177 meseci}

Citat:

honijat: I koji je to uslov koji mi govori kada pisem 2*k*pi a kada k*pi ?

Još malo pomoći.Ako znamo pravilo komutacije (3*5=5*3) onda ovu
gornju misteriju možemo napisati ovako:
I koji je to uslov koji mi govori kada pisem k*(2*pi) a kada k*(pi) ?
(A kada k*7,rekoh ja!)

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Odgovor na temu

honijat

Član broj: 231185
Poruke: 40
*.ptt.rs.

Profil

Re: Koeficient k u trigonometrijskoj jednacini

^{29.09.2009. u 16:56 - pre 177 meseci}

Sta zakon komutacije ima veze sa uslovom da pri pisanju resenja trig jednacine dodam ono 2*p*k ili samp pi*k. Mene zanima koji uslov zadatka mi govori da resenju zadatka naprimer pi/3 treba dodati 2*pi*k a zasto ne pi*k jer se u 2*pi nalazi i pi i ako je k tu samo zato da nam kaze da se resenje nalazi do beskonacno posle svakog perioda a nikad nemamo potrebu da ga zamenimo sa nekim celim brojem pa cemu onda to pisati i uvek naznaciti da k moze biti bilo koji ceo broj i pozitivan i negativan do u beskonacno?

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2154
*.broadband.blic.net.

+196 Profil

Re: Koeficient k u trigonometrijskoj jednacini

^{29.09.2009. u 17:56 - pre 177 meseci}

Pročitaj pažljivo ponovo pa ćeš shvatiti.
A onda ćeš znati da za rješenje nekih trig. jednadžbi netrebaš nikakvo
prokleto k,a ni 2k.Naprimjer za 2x+sinx=1.

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Odgovor na temu

honijat

Član broj: 231185
Poruke: 40
*.ptt.rs.

Profil

Re: Koeficient k u trigonometrijskoj jednacini

^{29.09.2009. u 19:13 - pre 177 meseci}

Neznam mozda me i ne razumes .Kod resenja pi/3+2*pi*k samo pi/3 je resenje a ovaj dodatak govori da se resenje nalazi posle svakog perioda u tacki pi/3 i to moramo da naznacimo da je to bezbroj ili k puta i da brojevi moraju biti celi i u minus i u plus . Pa cemu to kad je to bukvalno aksioma. I dali mozes malo jasnije da mi objasnis kako da znam kad treba pisati 2*pi a kada samo pi ostavimo po strani jednacine kojima to uopste ne treba.

_{[Ovu poruku je menjao honijat dana 29.09.2009. u 22:38 GMT+1]}

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2154
*.broadband.blic.net.

+196 Profil

Re: Koeficient k u trigonometrijskoj jednacini

^{29.09.2009. u 21:50 - pre 177 meseci}

kako da znam kad treba pisati 2*pi a kada samo pi
(kao da si nešto žestoko preskočio)

Trebaš znati koliki je period funkcije koju rješavaš.Najbolje da je skiciraš.Pa ako je period pi pišeš k*pi.Ako je 2pi piši 2kpi.Ako je 3pi piši 3kpi.Ako je 7
piši k*7.

Za periodičke funkcije vrijedi f(x)=f(x+P)=f(x+k*P). P je period.

Za funkciju y=sinx; P=2pi
Za funkciju y=tgx; P=pi
Za funkciju y=cos^2x; P=pi
Za funkciju y=cos4x; P=pi/2
Za funkciju y=ctg(pi/7(x)) P=7

Nacrtaj sam trig.krug pa se uvjeri.

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Odgovor na temu

honijat

Član broj: 231185
Poruke: 40
*.ptt.rs.

Profil

Re: Koeficient k u trigonometrijskoj jednacini

^{29.09.2009. u 22:20 - pre 177 meseci}

Evo kruznice a evo svake slike posebno pa ako imas strpljenja da mi objasnis kako sa slike mogu zakljuciti da ima ovaku ili onaku periodu

_{[Ovu poruku je menjao honijat dana 30.09.2009. u 14:04 GMT+1]}

Prikačeni fajlovi

Trig kruznica.jpg

Trig kruznica.jpg - 51.36k

Periode.jpg - 50.31k

Odgovor na temu

Cabo
Lokanje u bircuzu

Član broj: 10942
Poruke: 684
*.vdial.verat.net.

+5 Profil

Re: Koeficient k u trigonometrijskoj jednacini

^{30.09.2009. u 17:02 - pre 177 meseci}

Prosto objašnjenje, da prostije ne može biti:

Ako imaš neki faktor

kojim se množi argument trigonometrijske funkcije

, dakle

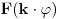
, onda se njen period deli tim faktorom. Na primer:

Funkcija

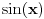
ima period

.

Funkcija

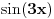
ima period

.

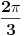
Funkcija

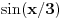
ima period

.

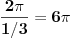
Uopšte, funkcija

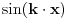
ima period

.

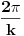
I što se zbunjuješ polarnim graficima kada je daleko lakše gledati „obične“ grafike trigonometrijskih funkcija, i periodi se daleko lakše uočavaju?

IZMENA: Sad sam malo bolje pročitao prve poruke. Izgleda da ti nije jasno šta je uopšte period funkcije. To je realni broj za koji funkcija, kada joj se argument sabere sa njim, ima istu vrednost kao i za početnu vrednost argumenta. Dakle, ako je

period funkcije

, onda mora da važi:

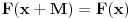
. To znači da će funkcija imati istu vrednost i za svako

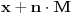
koje pripada domenu, u idealnom slučaju za sve

.

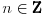
To da li se domen periodične funkcije zadaje sa ili bez „

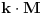
“, perioda, zavisi od uslova zadatka. Na primer, ako je eksplicitno rečeno da se funkcija

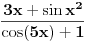
posmatra na segmentu

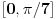
, onda ne dodaješ

„puta nešto“.

_{[Ovu poruku je menjao Cabo dana 30.09.2009. u 20:19 GMT+1]}

Kliknite da vidite kako da pišete matematičke formule u [tex]TeX[/tex]-u bez slanja slika

Odgovor na temu

honijat

Član broj: 231185
Poruke: 40
*.ptt.rs.

Profil

Re: Koeficient k u trigonometrijskoj jednacini

^{30.09.2009. u 20:17 - pre 177 meseci}

Cabo hvala na komentaru ali sad oped imam nedoumicu. Ja mislim da je perioda deo ugla ili nekakav ugao a da koeficient k govori koliko puta ga moze biti do u beskonacno ili u minus ili u plus.

_{[Ovu poruku je menjao honijat dana 30.09.2009. u 21:28 GMT+1]}

Odgovor na temu

Cabo
Lokanje u bircuzu

Član broj: 10942
Poruke: 684
*.vdial.verat.net.

+5 Profil

Re: Koeficient k u trigonometrijskoj jednacini

^{30.09.2009. u 20:33 - pre 177 meseci}

Neka je

periodična sa periodom

.

Dakle,

za

.

Uzmimo da posmatramo funkciju kojoj je argument pomnožen nekim faktorom

:

. Njoj je period

. Funkcija nema zadan poseban domen, pa možemo da množimo sa

koliko nam drago, drugim rečima možemo da sabiramo argument sa

.

Neka je

. Imamo:

. Šta imamo gore?

za

. Dakle, dobićemo

. To smo i hteli da dobijemo.

Kliknite da vidite kako da pišete matematičke formule u [tex]TeX[/tex]-u bez slanja slika

Odgovor na temu

honijat

Član broj: 231185
Poruke: 40
*.ptt.rs.

Profil

Re: Koeficient k u trigonometrijskoj jednacini

^{30.09.2009. u 21:04 - pre 177 meseci}

Ok kazes :Neka je F(x) periodicna sa M. moj problem i jeste kako da odredim vrednost za M.

Odgovor na temu

RMAN
Milan Đukić
student
Knićanin

Član broj: 32492
Poruke: 1166
*.zrlocal.net.

+5 Profil

Re: Koeficient k u trigonometrijskoj jednacini

^{01.10.2009. u 01:41 - pre 177 meseci}

Pa gledas u funkciju i razmisljas koji broj da stavis umesto

da bi dobio istu vrednost funkcije.

Na primer imas

i koja su resenja za x?

Kada je sinus jednak

? Jednak je za

ILI za

.

Ali nisu samo ovo resenja, ako na ova resenja dodas

,

,

,

opet ces doci na isti ugao sto znaci da je i ovo resenje.

Znaci resenja za x su

za svako

ili

za svako

_{[Ovu poruku je menjao RMAN dana 01.10.2009. u 02:56 GMT+1]}

_{[Ovu poruku je menjao RMAN dana 01.10.2009. u 09:42 GMT+1]}

Eureka!

MILAN DJUKIC
D J U K A

Odgovor na temu

miki069

Član broj: 161528
Poruke: 1951
212.200.34.*

+370 Profil

Re: Koeficient k u trigonometrijskoj jednacini

^{01.10.2009. u 08:10 - pre 177 meseci}

Mnogo je 11*pi/6.

Jednačina sin(x) = a gde je -1<=a<=+1 ima rešenja:

x=(alfa) + 2*k*pi i
x=(pi-alfa) + 2*k*pi

gde je alfa=arcsin(a)

Primer:
sin(x) = 1/2

ima rešenja:

x=pi/6+2*k*pi i
x=5*pi/6 +2*k*pi

alfa=arcsin(a) je osnovna vrednost alfe od -pi/2 do +pi/2 i treba je gledati sa trigonometrijskog kruga

Odgovor na temu

RMAN
Milan Đukić
student
Knićanin

Član broj: 32492
Poruke: 1166
*.zrlocal.net.

+5 Profil

Re: Koeficient k u trigonometrijskoj jednacini

^{01.10.2009. u 08:41 - pre 177 meseci}

Uh moja greska

. Ja sam 180 stepeni posmatrao kao

.
Eto sta se desava kad razmisljas u 3 ujutru

Ispravljeno je.....

Eureka!

MILAN DJUKIC
D J U K A

Odgovor na temu

[es] :: Matematika :: Koeficient k u trigonometrijskoj jednacini

Strane: 1 2 3

[ Pregleda: 14366 | Odgovora: 47 ] > FB > Twit

Srodne teme

14.04.2024. Re: Gde je Kejt? (samo pogrešni odgovori)
25.08.2007. Matematicki dokaz da je zena zlo
07.04.2006. Mordell-ova jednacina
19.03.2007. Nemoguci zadatak za 2 srednje elektrotehnicke
25.03.2007. Kako da vrednost iz nekog elementa u formi ostane..
06.06.2007. Hitno - Dva zadatka za maturski
30.06.2008. Trigonometrija,jos malo i gotovo ;)
23.02.2008. Recordi problem!??
03.04.2009. Izvodi, par opstih pitanja
05.04.2009. x+1=y-1 koliko je x, a koliko y

Navigacija

Lista poslednjih: 16, 32, 64, 128 poruka.