Mislim da mi je malo jasnije šta želiš da napraviš. Evo da probam kratko objašnjenje:
Nas zanima da li je sekvenca
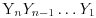
generisana nekim određenim izvorom (koji se karakteriše raspodelom verovatnoće da generiše određeni niz). Znači ovde nije bitno to što se računa moduo 26 niti išta s tim u vezi. Istina deo informacije se nepovratno gubi ali to je osobina svih „data processing“ zavisnosti.
Pretpostaviću da generator radi po funkciji:
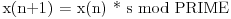
gde je PRIME fiksiran i poznat, a s je nepoznati „seed“ koji generiše raspodelu. Šta je ovde slučajno? Pa, kako ne možemo znati s unapred, to je verovatnoća da se pojavi recimo
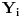
ako se pojavio
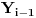
uslovljena izborom s. Pošto je funkcija deterministička, uslovna verovatnoća
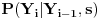
je uvek takva da je njena vrednost 1 za neki par
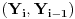
kada fiksiramo neko s. E sad, ovu raspodelu možemo lako dobiti empirijski, tako što uzmemo algoritam generatora slučajnih brojeva iz standardne C biblioteke i zapišemo u niz tabela, za različito s, koje se sekvence
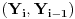
javljaju. Tako dobijemo empirijsku raspodelu
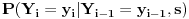
, a nama treba da izračunamo
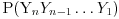
Ostatak posla je mehanika koja treba da svede ovaj prethodni izraz (verovatnoću da je generisan baš dati niz) na nešto što je izraženo samo u funkciji onih empirijskih raspodela.
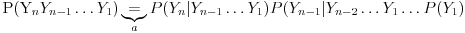
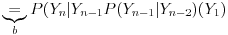
gde (a) dolazi kao posledica primene lančanog pravila, a (b) kao posledica toga što smo modelovali generator kao Markovljev proces, tj. trenutno stanje zavisi samo od prethodnog. Ovde naravno očekujemo da susedni slučajni brojevi nisu nezavisni, što bi trebalo da bude ispunjeno. Kada je alfabet binarni a generator pseudoslučajan sa povratnom spregom (klasičan elektroničarski pseudo-random generator) takva korelacija postoji, ali za ne-binarni alfabet ne znam tačno kako izgleda, možda može negde da se pronađe.
Ostaje nam da svedemo poslednji proizvod na empirijsku raspodelu.
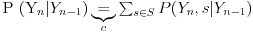
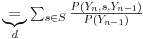
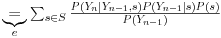
c: obrnuta marginalizacija
d: Bajesovo pravilo o uslovnim verovatnoćama
e: malo gimnastike sa gornjim izrazom
Na kraju se dakle dobije verovatnoća izražena u funkciji raspodela koje se mogu empirijski oceniti, i to su sve ove uslovne raspodele u poslednjem izrazu. Mnoge od ovih stvari se mogu unapred sračunati, verujem da ti to neće biti problem.
E sad, kako izmeriti da li je to „dovoljno“ random? (randome, nisam te prozvao!:)) Ja bih ponovio istu ovu računicu, samo sa empirijskom raspodelom za neki prirodni jezik i zatim napravio log-likelihood (sad se ne sećam kako se to po naški kaže, valjda log-poverenje) meru:
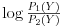
što je standardan način da se uporede dve verovatnoće. Tu će se ponešto od izraza srećom skratiti pa ćeš dobiti jednostavniju formulicu za računanje. Ako log pretegne u pozitivnu stranu, onda je prva verovatnoća veća (ako uzmeš da je
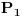
verovatnoća da niz pripada jednoj raspodeli, npr. raspodeli iz srpskog jezika, a
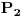
verovatnoća da niz pripada drugoj raspodeli, npr. slučajnoj).
Naravno, što duži uzorak to je bolje. Ne znam koliko će ovo biti dobro za kratke sekvence. Možeš probati ono što si i sam rekao, da pronađeš empirijske raspodele za tri i(li) više znakova, koliko god je moguće. Primeti da smo u teoriji mogli izračunati i direktno empirijsku raspodelu za Y, ali da to u praksi nije moguće jer je prostor mogućih vrednosti veliki
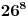
. Upravo zato smo i koristili svu ovu gimnastiku - da bismo pokušali da smanjimo posao.
f