[es] - Neprekidnost operatora

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.dynamic.sbb.rs.

+33 Profil

^{02.02.2009. u 14:21 - pre 197 meseci}

Treba mi malo pomoci oko matematicke strogoce. Evo nesto na sta sam nabasao i moram priznati da me je zbunilo... Unapred hvala na odgovoru!

http://www.svijetfizike.com/

Prikačeni fajlovi

Neprekidnost operatora.pdf - 24.33k

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.sbb.rs.

+2801 Profil

Re: Neprekidnost operatora

^{02.02.2009. u 16:09 - pre 197 meseci}

Sta ti je operator koordinate? Da li je to projekcija na jednu od koordinatnih osa (

)? Ako je tako, onda je

njegov spektar.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.dynamic.sbb.rs.

+33 Profil

Re: Neprekidnost operatora

^{02.02.2009. u 16:49 - pre 197 meseci}

Ova tema pocinje s njim!
http://www.elitesecurity.org/t334007-0-Delta-distribucija

http://www.svijetfizike.com/

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.sbb.rs.

+2801 Profil

Re: Neprekidnost operatora

^{03.02.2009. u 10:53 - pre 197 meseci}

Kad govoris o ermitskim operatorima, onda radis u Hilbertovom prostoru. Sto se tice funkcionalnih prostora, takav je Lebegov prostor

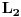
. No, proizvod

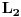
funkcije sa

ne mora obavezno biti

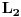
funkcija. Takodje, ovde radis u Lebegovom prostoru posecenom po relaciji "jednako skoro svuda".

Zapravo, za merljiv prostor

i merljivu funkciju

je proizvod funkcije

sa ma kojom funkcijom iz

funkcija iz

akko je

. Dakle, tebi u slucaju kada je

merljiv podskup od

treba da funkcija

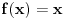
bude esencijalno ogranicena, a to je slucaj tacno onda kada je

ogranicen skup, a spektar je tacno zatvorenje skupa

, pa je u tom slucaju spektar zaista i ogranicen.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.dynamic.sbb.rs.

+33 Profil

Re: Neprekidnost operatora

^{03.02.2009. u 12:24 - pre 197 meseci}

Ono sto mene jos zanima ako mozes da mi odgovoris je sledece. Dakle ta prekidnost se ogleda u tome sto mnozenjem

sa nekom funkcijom

koja je iz

mozes da dobijes funkciju koja nije iz

. Da li si ti to video odmah iz sv. problema:

Posto se dobija

koja nije iz

. Odnosno da li je svaki operator s neprekidnim spektrom prekidan?
I da li mozes da navedes primer neke neprekidne funkcije

za koju vazi da

nije iz

?

Hvala na odgovoru!

http://www.svijetfizike.com/

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.sbb.rs.

+2801 Profil

Re: Neprekidnost operatora

^{03.02.2009. u 13:55 - pre 197 meseci}

ne pripada prostoru

. Tu su samo merljive funkcije (dakle, obicne funkcije, ne distibucije), ciji je integral kvadrata modula konacan.

To sto mnozenjem funkcije koja pripada prostoru dobijas nesto sto ne pripada prostoru znaci da taj operator pre svega nije definisan u nekim tackama, bar sa tim izborom i kodomena, tj. da to uopste nije preslikavanje sa tim domenom i tim kodomenom.

Funkcija

pripada prostoru

, ali funkcija

ne pripada prostoru

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.dynamic.sbb.rs.

+33 Profil

Re: Neprekidnost operatora

^{03.02.2009. u 13:59 - pre 197 meseci}

Citat:

Nedeljko:

ne pripada prostoru

. Tu su samo merljive funkcije (dakle, obicne funkcije, ne distibucije), ciji je integral kvadrata modula konacan.

Citat:

petarm: Ono sto mene jos zanima ako mozes da mi odgovoris je sledece. Dakle ta prekidnost se ogleda u tome sto mnozenjem

sa nekom funkcijom

koja je iz

mozes da dobijes funkciju koja nije iz

. Da li si ti to video odmah iz sv. problema:

Posto se dobija

koja nije iz

To sam i rekao!

Citat:

Nedeljko:
To sto mnozenjem funkcije koja pripada prostoru dobijas nesto sto ne pripada prostoru znaci da taj operator pre svega nije definisan u nekim tackama, bar sa tim izborom i kodomena, tj. da to uopste nije preslikavanje sa tim domenom i tim kodomenom.

Funkcija

pripada prostoru

, ali funkcija

ne pripada prostoru

Hvala!

http://www.svijetfizike.com/

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.sbb.rs.

+2801 Profil

Re: Neprekidnost operatora

^{03.02.2009. u 14:03 - pre 197 meseci}

Mnozenjem merljive funkcije sa x ne mozes dobiti Dirakovu distribuciju, vec merljivu funkciju.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.ADSL.neobee.net.

+33 Profil

Re: Neprekidnost operatora

^{04.02.2009. u 14:20 - pre 197 meseci}

To se slazem ali kad radis sv. problem operatora koordinate kao resenje dobijas

fju.

http://www.svijetfizike.com/

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.sbb.rs.

+2801 Profil

Re: Neprekidnost operatora

^{04.02.2009. u 16:13 - pre 197 meseci}

Ne mozes kao sopstveni vektor dobiti nesto sto nije vektor, tj. sto ne pripada tom prostoru. Nikakva

distribucija ne pripada Lebegovom prostoru. Dirakovu distribuciju mozes dobiti iskljucivo ako radis problem sopstvenih vrednosti operatora u prostoru Distribucija, ali to nije Hilbertov prostor, pa ne mozes govoriti o samoadjungovanosti. Moras imati kompletnu korektnu formulaciju zadatka, a ne samo neke parcice, inace dobijas matematiku poput fizike nekih ucesnika teme o teoriji relativnosti foruma za fiziku ES-a.

U prostoru distribucja je za ma koju beskonacno diferencijabilnu funkciju

korektno definisan linearan operator

U slucaju da je

, sopstveni vektor tog operatora je Dirakova distribucija, ali prostor distribucija ne obrazuje Hilbertov prostor, pa ovaj slucaj ne odgovara formulaciji tvog zadatka u kome se pominje pojam smoadjungovanog operatora.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.ns.ac.yu.

+33 Profil

Re: Neprekidnost operatora

^{05.02.2009. u 16:17 - pre 197 meseci}

Vidi ovako svojstveni problem operatora koordinate je

Posto ermitski operatori imaju realne svojstvene vrednosti, a sv. vrednost je rezultat merenja ja uzimam da je ovaj operator ermitski. Odnosno:

I to je zaista tako.

distribucija nije u

, ali jeste u

, gde je

tzv. Rigid Hilbert space.

http://www.svijetfizike.com/

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.sbb.rs.

+2801 Profil

Re: Neprekidnost operatora

^{06.02.2009. u 07:52 - pre 197 meseci}

Definisi mi taj Rigid Hilbert space.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.ADSL.neobee.net.

+33 Profil

Re: Neprekidnost operatora

^{06.02.2009. u 18:52 - pre 197 meseci}

http://www.elitesecurity.org/t299472-0#1792299

Ovde se vec raspravljalo o njemu!

http://www.svijetfizike.com/

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
195.222.97.*

+2801 Profil

Re: Neprekidnost operatora

^{07.02.2009. u 15:09 - pre 197 meseci}

Ja tamo vidim samo neku svađu. Da li bi mogao da napišeš formalnu definiciju od RHS?

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.ADSL.neobee.net.

+33 Profil

Re: Neprekidnost operatora

^{08.02.2009. u 11:49 - pre 197 meseci}

Rigid Hilbert space je uredjena trojka

, gde je

Hilbertov prostor koji je gust u

, a

je njegov dual. U

nalazice se

-funkcija.

http://www.svijetfizike.com/

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.sbb.rs.

+2801 Profil

Re: Neprekidnost operatora

^{09.02.2009. u 10:35 - pre 197 meseci}

Ako je

gust Hilbertov potprostor Hilbertovog prostora

, onda je

. Pravis li razliku izmedju predhilbertovog prostora (vektorskog prostora sa skalarnim proizvodom) i Hilbertovog prostora (kompletnog predhilbertovog prostora)?

Kompletan potprostor normiranog prostora je uvek njegov zatvoren potprostor, a zatvoren gust potprostor normiranog potprostora je ceo prostor.

Cak i u slucaju da je

, sta ti je

, tj. koji Hilbertov prostor?

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.dynamic.sbb.rs.

+33 Profil

Re: Neprekidnost operatora

^{07.08.2009. u 22:49 - pre 191 meseci}

Da budem precizniji uredjena trojka

http://www.svijetfizike.com/

Odgovor na temu