Hajde da se sad ispravim do kraja.
Implikacija
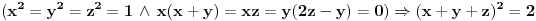
je tacna, jer je tacna za ma koje vektore
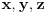
. Zaista, premisa je uvek netacna (jer je sistem uslova protivrecan), pa je implikacija tacna, jer je

tacno bez obzira na istinitosnu vrednost iskaza

. Na taj nacin treba shvatiti izvodjenje koje sam prvo dao. Rezultat je
tacno tvrdjenje, s tim sto ga treba pravilno interpretirati. No, recimo da nas zanima da li taj sistem uslova ima resenja.
Prvo, uslovi
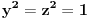
,
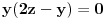
su ekvivalentni uslovima
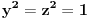
i
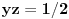
. Na osnovu nejednakosti Minkovskog mora biti
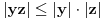
, sto je i ispunjeno i to je dovoljno da se ovaj sistem uslova moze zadovoljiti. No, obzirom da je
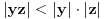
, vektori
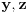
su linearno nezavisni. Neka je

ortogonalna projekcija vektora

na potprostor odredjen vektorima
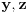
tj. za neke skalare
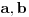
vazi
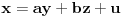
i
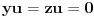
, skalarnim mnozenjem vektora

sa
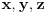
dobijamo da je
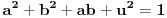
,
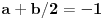
,
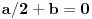
. Odavde se lako nalaze
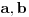
, a onda se iz prve jednacine vidi da nema resenja. Zavrsicu ovo malo kasnije.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.