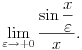Hevisajdova funkcija je neprekidna u svim tackama osim u jednoj, u cijoj je okolini ogranicena, iz cega sledi da je lokalno integrabilna. Odatle sledi da ona indujuje je jednu regularnu distribuciju.
.
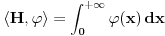
Citat:
petarm: Mozes li ovo pokazati?
Neka je
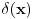
trazena funkcija i neka je segnemt
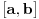
takav da ne sadrzi nulu. Neka je
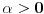
i
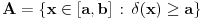
. Skup
je merljiv, jer je funkcija
merljiva kao lokalno integrabilna. Stoga, za svako
postoji zatvoren skup
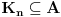
takav da je
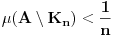
. Taj skup je kao zatvoren i ogranicen kompaktan. Takodje, postoji otvoren skup
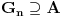
takav da je
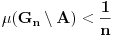
. Bez umanjenja opstosti mozemo jos pretpostaviti da je
,
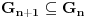
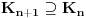
i da
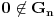
. U knjizi "Parcijalne jednacine" Boska Jovanovica se moze naci primer funkcije
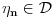
takve da je
,
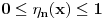
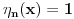
za
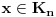
i
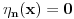
za
.
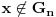
Posto je
lokalno integrabilna funkcija, vazi
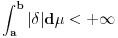
, pa posto je
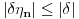
i
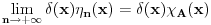
skoro svuda, gde je
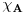
funkcija koja je jednaka jedinici u tackama skupa
,a u ostalim tackama je jednaka nuli, Lebegov stav o dominantnoj konvergenciji se moze primeniti, pa je
.
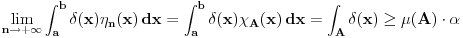
Sa druge strane je
,
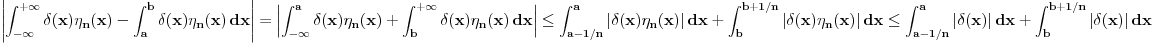
sto je zbog lokalne integrabilnosti funkcije
za dovoljno veliko
manje od zadatog
. No, zajedno sa
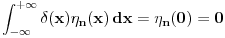
odatle sledi da je
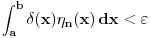
za dovoljno veliko
, pa je
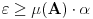
. Posto je
proizvoljno, odatle sledi (zbog
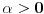
) da je
.
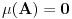
Znaci, za svako
vazi da je
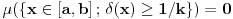
, pa je i skup
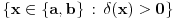
mere nula kao prebrojiva unija skupova mere nula. No, segment
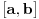
je bio proizvoljan segment koji ne sadrzi nulu, pa posto je
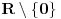
prebrojiva unija takvih intervala, bice
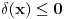
skoro svuda na
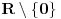
, pa samim tim i na skoro svuda na
jer je jednoclan skup mere nula. Na slican nacin se moze dokazati i da je
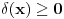
skoro svuda, odakle je
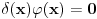
skoro svuda za ma kakvu funkciju
odakle je
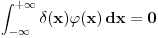
suprotno polaznoj pretpostavci.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
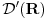Limes u prostoru distribucija
?
Ima dosta pretpostavki. Prva je da vazi Fubini...
