[es] - Turnir Gradova

nikmil

Član broj: 45895
Poruke: 55
*.crnagora.net.

Profil

^{06.04.2008. u 20:54 - pre 207 meseci}

Evo zadataka za kvalifikacije za Turnir Gradova: http://www.filecrunch.com/file...38a6921deb0f&fileId=136445

Uspio sam da rijesim 1, 2, 4 i 6. Rjesenja cu postovati brzo, dok ih skeniram. Treba mi pomoc oko 5. zadatka. Evo teksta:

5. Svi pozitivni cijeli brojevi napisani su u jednom redu po nekom redosledu (svaki broj pojavljuje se tacno jednom). Da li obavezno postoji nekoliko (vise od jednog) brojeva
napisanih uzastopno (pocevsi od nekog mjesta) cija je suma prost broj?

Mislim da je poenta u tome da se napravi takav redosled gdje zbirovi bilo kojih susednih brojeva nisu prosti. Pitanje je kako... :(
Takodje za 7. zadatak, mislim da je lose preveden sa engleskog, pa bih zamolio nekoga da to provjeri.

Prikačeni fajlovi

vs29os-a.pdf - 63.81k

Odgovor na temu

nikmil

Član broj: 45895
Poruke: 55
*.crnagora.net.

Profil

Re: Turnir Gradova - Zadaci

^{08.04.2008. u 16:46 - pre 207 meseci}

Evo i resenja. U djvu formatu su, zbog velicine (pdf mi ispadne preko 6mb).

Prikačeni fajlovi

rjesenja.djvu - 611.47k

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.dynamic.sbb.rs.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: Turnir Gradova - Zadaci

^{08.04.2008. u 23:21 - pre 207 meseci}

Citat:

nikmil:
Mislim da je poenta u tome da se napravi takav redosled gdje zbirovi bilo kojih susednih brojeva nisu prosti. Pitanje je kako... :(

Taj redosled možeš lako napraviti na sledeći način: uzmeš da je prvi član niza jednak

, i svaki sledeći neka bude najmanji broj takav da nikoji zbir uzastopnih brojeva koji se završavaju s tim novododatim nije prost. Ovo je uvek moguće: zaista, ako si već upisao

brojeva i ako je

njihova suma, gornje ograničenje za sledeći jeste

.

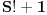
E sad, problem s ovim rešenjem jeste u tome što niko ne garantuje da ćemo na ovaj način pokupiti sve prirodne brojeve. U prilogu imaš spisak s prvih 10.000 članova ovako konstruisanog niza, pa vidi možeš li da uočiš neku pravilnost.

Citat:

nikmil:
Takodje za 7. zadatak, mislim da je lose preveden sa engleskog, pa bih zamolio nekoga da to provjeri.

I engleska postavka je pogrešna, Rusi su naknadno poslali ispravku (imaš i to u prilogu). Greška je samo u tome što umesto „dve prave“ treba da piše „tri prave“.

Ljubičice crvena, što si plava kô zelena trava.

Prikačeni fajlovi

niz.txt - 60.38k

Ispravka.gif - 112.57k

Odgovor na temu

nikmil

Član broj: 45895
Poruke: 55
195.66.191.*

Profil

Re: Turnir Gradova - Zadaci

^{09.04.2008. u 09:28 - pre 207 meseci}

Hvala puno! Malo ću meditirati na temu ovog zadatka, pa ću javiti ako nađem nešto zanimljivo.
Pošto vidim da si upućen, šta je ustvari taj Turnir Gradova? Gdje i kad se održava? Našao sam na internetu neku stranu, ali nije baš bogata informacijama. Date su neke propozicije turnira: koliko se sati radi, da je dato 7 zadataka, od kojih ti biraš 3 koja ćeš da uradiš, itd. Ovdje (u CG) PMF sastavlja ekipu za međunarodna takmičenja, pa su mi poslali ove zadatke (i još neku pripremnu varijantu zadataka) i rekli da upadam u ekipu ako uradim jedan. Tako da sam ja shvatio da su ovo kvalifikacioni zadaci. Smijem li uopšte da ja postujem ove zadatke i rešenja, pošto negdje možda i nisu završene kvalifikacije?

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.dynamic.sbb.rs.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: Turnir Gradova - Zadaci

^{09.04.2008. u 21:47 - pre 207 meseci}

Održava se u Rusiji na jesen. Prethodno se održavaju kvalifikacije (svako u svojoj zemlji, štaviše po školama), i to su ovi zadaci koje si poslao. Njih svi rade u isto vreme (i to je bilo još pre mesec dana), pa slobodno možeš stavljati zadatke i rešenja, ne moraš se bojati da negde to još nije završeno.

Jedino je pitanje za kakva međunarodna takmičenja vaš PMF sastavlja ekipu s ovim zadacima. Možda je baš Turnir gradova (i u tom slučaju je trebalo da ovo radite još pre mesec dana, u učionici, a ne kod svoje kuće; ovako vas Rusi mogu diskvalifikovati ako nešto posumnjaju, a nadajte se da neće), a možda je u pitanju neko drugo takmičenje (npr. IMO) pa su vaši nadležni samo iskoristili ove zadatke umesto da sastave svoje.

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

nikmil

Član broj: 45895
Poruke: 55
85.94.113.*

Profil

Re: Turnir Gradova - Zadaci

^{10.04.2008. u 09:55 - pre 207 meseci}

Dobili smo ove zadatke i rok od 2 dana da ih uradimo i pošaljemo rešenja. To je za ekipu za Turnir gradova, i radili smo ih, tako otprilike, prije nekih mjesec dana. Ali ih je svako radio kod svoje kuće, tako da te molim da brišeš ovo prije nego što neki Rus vidi :)

Odgovor na temu