Nemam puno vremena ali cu ti pokusati odgovoriti na pitanje broj 1.
Svaki BIpartitni graf je 2-obojiv. Evo uzmimo npr
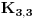
ili uopsteno
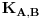
. On izgleda ovako
(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6) = P gdje su
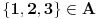
i
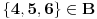
cvorovi a notacija
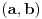
veza izmedju tacaka a i b.
Algoritam je jednostavan.
Provjeravas sve parove. Ako za sve parove iz P postoji jedan par (a, b) gde je
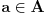
i
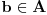
onda graf nije 2-obojiv. Zasto? Evo zasto. Recimo da je u P jedan par (1,2) onda imamo sljedece stanje
(1, 2) (1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6) = P
Za prvi par (1, 2) bojimo 1 sa crvenom, 2 sa plavom.
(1, 4) 1. ostaje crvena, 4 bojimo sa plavom
...
(2, 4) postoji kolizija jer 2 je obojeno sa plavom i 4 obojeno sa plavom, moramo dodati jos jednu farbu sto u ovom slucaju graf nije 2-bojiv.
Nadam se da si skontao u cemu je problem.
To sam samo naveo za bipartitne grafove, a za ostale nije isto problem skonati mada sad nemam vremena nesto posebno
Uzdravlje
Amel
Scanner
algoritmi vezani za grafove
