Znacenje fja stanja u kvantnoj mehanici

Sta predstavljaju tacno fje stanja u kvantnoj mehanici? Koja je njihova fizicka interpretacija? Njihov kvadrat predstavlja verovatnocu. Zasto operatori impulsa i koordinate deluju bas na ove fje? Hvala unapred na odgovoru.

---

Talasne funkcije sadrze sve podatke o datoj varijabli koje mi u odredenom trenutku mozemo da znamo o toj varijabli. Sama talasna funkcija nema fizicku interpretaciju. Njena veza sa realnoscu je upravo preko kvadrata amplitude koja predstavlja verovatnocu nalazenja cestice u nekoj tacki prostora u datom trenutku.Zato sto je to funkcija impulsa i koordinate.

A zasto se tvrdi da su te fje stanja koje nemaju fizicki smisao ortogonalne?

---

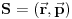
Izložiću jednu priču koja ne odslikava istorijski razvoj problema, već jedan deduktivan pristup baziran na našem današnjem znanju. Pre nego što počnem da pričam o stanjima u kvantnoj mehanici, da se dotaknem malo klasične mehanike. U klasičnoj mehanici stanje čestice je u potpunosti određeno dvema funkcijama, njenim položajem i impulsom, tj. stanje čestice je . Prostor stanja čestice čini skup svih mogućih stanja, tj. to je neki realni šestodimenzionalni prostor. Sve fizičke veličine, tj. varijable u klasičnoj mehanici su analitičke funkcije položaja i impulsa, i one se mogu koristiti podjednako dobro za karakterisanje stanja čestice u klasičnoj mehanici umesto položaja. Takođe treba uočiti da, iako klasični prostor stanja može imati vrlo zanimljivu topološku strukturu, sa algebarske tačke gledišta on nema nikakve posebne osobine.

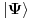
Ispostavlja je da je preispitivanje prirode prostora stanja krucijalan korak ka prelasku sa klasične na kvantnu mehaniku. Da bismo našli kvantni analogon klasičnom stanju, presudna je pretpostavka da je kvantni prostor stanja vektorski prostor. Tj. stanje u kvantnoj mehanici, je nekakva apstraktna veličina koju mi ne možemo zamisliti i za koju znamo da može na neki, takođe apstraktan, nama nepoznat način da se sabira i daje veličinu koja će takođe predstavljati stanje sistema. To je algebarska osobina koju klasični prostor stanja ne poseduje (uzmi na primer česticu koja se kreće po kružnici i neka se položaj čestice meri u odnosu na centar te kružnice, a zatim probaj da sabereš te vektore i vidi da li ćeš dobiti vektor čiji vrh leži na kružnici).

Međutim, samo poznavanje činjenice da su stanja vektori ti ne pomaže mnogo. Mi želimo neku prediktivnu moć, a za to nam je neophodno da umemo da računamo, tj. da te vektore prevedemo u brojeve. Ovde se treba malo zaustaviti i razmisliti šta u stvari računanje sa vektorima znači. Vektori, kako smo ih učili u osnovnoj školi predstavljaju obične orijentisane linije i naučili smo još tada kako da koristimo pravilo paralelograma da bismo ih sabirali. Ovde su sve to apstraktne operacije koje nisu ni u kakvoj vezi sa brojevima. Da bismo računali sa njima, moramo nekako da ih predstavimo brojevima. To smo radili tako što smo fiksirali koordinatni sistem, tj. birali tri ortogonalna vektora jednake dužine, koju smo proglasili jediničnom, potom projektovali naš vektor na ta tri vektora i merili koliko puta su te projekcije duže ili kraće u odnosu na vektor na koji su projektovane. Te odnose smo proglašavali koordinatama vektora te smo tako dobili efektan način da našu apstraktnu notaciju vektora kao orijentisanih strelica prevedemo u poznatu notaciju uređene trojke realnih brojeva. Potom smo pronašli način kako da pravilo paralelograma prevedemo u algebarske operacije sa trojkama realnih brojeva. Ono što se ovde desilo je nešto što se zove reprezentovanje i ključno je za bilo kakav rad sa vektorima. Da napomenem ovde još nekoliko stvari. Prvo, izbor koordinatnog sistema tj. bazisa je bio prepušten nama, tj. on nije menjao vektore same po sebi, već samo njihovu brojnu reprezentaciju. Poznajući odnos između dva bazisa, sasvim je lako određenu brojnu reprezentaciju vektora prevesti u brojnu reprezentaciju koja odgovara drugom bazisu. Takođe, da smo uzeli bazis sa dva vektora javila nam bi se nejednoznačnost pri reprezentaciji, naime, da smo uzeli bazis samo duž x i y ose, svi vektori sa istom x i y projekcijom bi se reprezentovali istom trojkom brojeva. Takođe, to što smo uzeli ortogonalne vektore iste, jedinične dužine je važno sa fizičke strane, zato što želimo da svi pravci budu podjednako važni i da se duž svakog pravca meri istom jedinicom.

Sada nazad na kvantnu mehaniku. Dakle, pretpostavili smo da je kvantni prostor stanja neki krajnje apstraktan prostor stanja i potreban nam je nekakav način da stanja reprezentujemo brojevima i pri tome dozvoljavamo da se stanja reprezentuju kompleksnim brojevima. Za reprezentaciju nam je potreban neki "koordinatni sistem", tj. bazis. Koordinatni sistem je u prethodnoj rečenici pod navodnicima zato što on nema nikakve veze sa koordinatnim sistemom, onakvim kakav nam je poznat iz fizike. To su prosto neka stanja koja smo izdvojili i koja nam služe da projektujemo ostala stanja na njih i potom da odnose "dužine" tih projekcija sa "dužinama" stanja na koja su projektovani proglasimo brojnom reprezentacijom stanja. Kako izdvojiti ta stanja? Tu u igru ulaze položaj i impuls. Prilikom prelaska na kvantnu mehaniku pravi se još jedna pretpostavka, a to je da sve klasične varijable, koje su bile analitičke funkcije prelaze u linearne operatore i to ne bilo kakve, već hermitske. Ovde je sada već teško, a ne služiti se matematikom, ali ono što je bitno je da hermitski linearni operatori imaju realne svojstvene vrednosti i ortonormirani svojstveni bazis. To nekome ko nije matematičar ili nije student druge godine fizike verovatno ništa ne znači, ali u prevodu to znači da postoji proces kojim je svaki hermitski operator jednoznačno povezan sa nekim realnim brojevima i skupom nekih vektora koji su međusobno ortogonalni i jedinične dužine. Ovo će zapravo značiti sledeće: u kvantnoj mehanici su sve fizičke veličine, tj. opservable, predstavljene hermitskim linearnim operatorima koji deluju u prostoru stanja; pri tome, svojstvene vrednosti predstavljaju moguće rezultate merenja fizičke veličine čijem operatoru te svojstvene vrednosti pripadaju; takođe, postojanje ortonormiranog svojstvenog bazisa znači da imamo ono što nam treba da bismo jedinstveno i sa fizičkim smislom reprezentovali naša stanja.

Izaberimo zato svojstveni bazis operatora položaja kao bazis pomoću kojega ćemo reprezentovati stanja. Ovaj bazis ima bitnu osobinu da daje jednoznačnu reprezentaciju (setite se gornjeg primera sa bazisom samo duž x i y ose). Takođe je i ortonormirarn, a gore sam objasnio zašto fizičari vole ortonormirane bazise. Samo, ovde valja voditi računa da ta ortonormiranost nije geometrijska, već je ortonormiranost u prostoru stanja i ona proizilazi iz skalarnog proizvoda (kažemo da su vektori čiji je skalarni proizvod 0 po definiciji ortogonalni), a ne iz neke geometrijske ideje o vektorima pod uglom od 90 stepeni. Takođe, skup svojstvenih vrednosti operatora položaja je ceo skup trojki realnih brojeva, što znači da prilikom merenja položaja čestice možemo dobiti bilo koju trojku realnih brojeva. 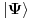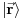Kada isprojektujemo stanja na svojstvene vektore operatora položaja , a projekcije su u stvari skalarni proizvodi, (pošto u apstraktnom prostoru stanja nemamo notaciju normala i preseka) dobićemo kompleksne brojeve, koji ako se posmatraju kao funkcije koordinata u stvari predstavljaju ono što se naziva talasnom funkcijom, tj. . 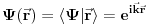Dakle, talasne funkcije su u stvari stanja u tzv. koordinatnoj reprezentaciju. Što se pridavanja fizičkog značaja stanju u kvantnoj mehanici tiče, problem se sastoji u tome da nađemo operaciju kojom apstraktnoj veličini pridružujemo neki realan broj. 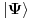Kako su stanja vektori, mi upravo imamo jednu takvu operaciju, a to je skalarni proizvod . 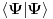Pokazuje se da u koordinatnoj reprezentaciji skalarni proizvod izgleda kao kvadrat modula kompleksnog broja . 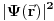Odatle i fizička interpretacija koju je predložio Born: Kvadrat modula talasne funkcije predstavlja verovatnoću da se čestica nađe u stanju koje ta talasna funkcija predstavlja.

Kada bismo na primer, umesto operatora položaja prešli na operator impulsa i stanja reprezentovali u njegovom svojstvenom bazisu, ono što je u notaciji talasnih funkcija bio ravan talas, u impulsnoj reprezentaciji bi se pretvorilo u Dirakovu delta-funkciju. Ovo sa matematičke strane radikalno menja stvari, ali fizički se ništa ne menja. Stvar je bila prosto u tome da smo promenili "koordinatni sistem", a kao što znamo, to u fizici ne sme ništa da menja.

_{[Ovu poruku je menjao tomkeus dana 14.06.2007. u 23:45 GMT+1]}

Kolega je skoro sve rekao. Treba napomenuti da se taj apstraktni prostor naziva Hilbertov beskonacno domenzioni prostor. A kako je beskonacno dimenzioni prostor, to u njemu mozemo kreirati beskonacno mnogo ortonormiranih sistema. Bilo koji ne ortonormirani bazis mozemo prevesti u ortonormirani specijalnim tehnikama, kao Smitov postupak ortogonalizacije. Jedan ortonormirani sistem cini kompletan skup talasnih funkcija te proizvoljnu talasnu funkciju u njemu mozemo predstaviti kao njihovu linernu kombinsciju, analogno predstavljanju vektora preko zbira 3 nezavisna(ortogonalna) vektora. Odavde sledi jos jedna osobina talasne funkcije. Tj. ako dve talasne funkcije opisuju stanje sistema, onda bilo koja njihova linearna kobinacija opisuje stanje tog sistema.
Jos treba naglasiti da Talasna funkcija nije slucajno uzeta kao kompleksna funkcija. To je uradeno iz potreba da se teorija slozi sa experimentanim podacima dualnosti i neodredenosti polozaja cestica.

To sto je talasna fja uzeta kao kompleksna ima veze i s tim sto u Sredingerovoj jni figurise imaginarna jedinica? Kako se uopste doslo do Sredingerove jne? Jer njena resenja su te tzv talasne fje, zar ne?

---

Do Šredingerove jednačine se došlo kao i do većine fundamentalnih teorija u fizici: metodom uzaludnih pokušaja i srećnog nagađanja. To što se na fakultetu sve uči lepo spakovano i strukturisano je došlo iz godina razvoja i popunjavanja logičkih rupa posle nečijeg srećnog nabadanja prave formule. Kada bismo morali da učimo fiziku iz originalnih radova njenih tvoraca studiranje bi bilo skoro nemoguće (ako do sada nisi pročitao neki od klasičnih radova preporučujem ti da to uradiš i da malo osetiš kako se stvara nauka - preporučio bih ti Plankov rad iz 1901. o spektru apsolutno crnog tela).

Ono čime se Šredinger, koliko je meni poznato, vodio bilo je ono što je znao iz elektrodinamike o talasima i o zakonima održanja. Verovatno je posmatrao kompleksnu formu ravnih talasa pokušavajući tako da modelira deBroljevu talasnu hipotezu. Vodeći se zakonima održanja verovatno je pokušao sa nekoliko formi talasnih jednačina. To ga je verovatno dovelo do jednačine za slobodnu jednodimenzionalnu česticu . Ovo je ujedno i najprostija forma talasne jednačine koja daje odgovarajuću disperzionu relaciju za impuls i energiju. Kako je ubacio potencijal u ovo, e o tome već nemam predstavu.

Zanimljivo je, međutim, videti kako ovo funkcioniše u okviru moderne mašinerije kvantne mehanike. Pođimo od toga da je stanje sistema u trenutku t jednoznačno (ovime smo se pozvali na kauzalnost evolucije što je nešto logično, jer ako bismo se odrekli kauzalnosti, morali bismo da se odreknemo fizike) povezano sa stanjem u početnom trenutku pomoću evolucionog operatora na sledeći način . Ovo znači da evolucioni operator deluje tako što izevoluira početno stanje u vremenski trenutak koji je zadat kao njegov parametar. Razmotrimo sada infinitezimalnu evoluciju iz stanja u stanje . Veza između ova dva stanja pomoću evolucionog operatora je pošto prelazimo iz stanja u trenutku t u stanje u koje sistem došao posle infinitezimalnog vremena dt koje je približno početnom stanju. Ako posmatramo stanje u trenutku t+dt kao funkciju vremena možemo ga razviti oko trenutka t . Ako ovo stavimo u prethodnu jednačinu i malo sredimo dobićemo , gde je jedinični operator. Pošto evolucioni operator predstavlja malu evoluciju, tj. povezuje skoro ista stanja možemo ga napisati kao gde jedinični operator predstavlja evoluciju za nulto vreme, je neki operator i on je pomnožen sa infinitezimalnim vremenom dt da bi dao malu popravku na nultu evoluciju. Zamenom u prethodnu jednačinu se dobija što trivijalnim transformacijama daje što je poznato kao Šredingerova jednačina. Imaginarna jedinica i redukovana plankova konstanta su ubačene da bi evolucioni operator bio unitaran i da bi dimenzije bile odgovarajuće, respektivno. Unitarnost nam je potrebna da bi se u toku evolucije održavala norma vektora, tj. da bismo imali konzistentnu statistiku u različitim vremenskim trenucima. Što se dimenzija tiče, izrazimo prvo operator evolucije preko vremena i operatora na sledeći način. Totalni diferencijal evolucionog operator je dat sa , gde sam iskoristio da je , tj. evolucija za t+dt je rezultat dve uzastopne evolucije, prvo za t, a potom za još dt. Ako se sada izrazi evolucija za dt preko operatora i vremena dobija se diferencijalna jednačina za evolucioni operator što integracijom daje , gde je korišćen početni uslov . Ovde sada vidimo da u argumentu eksponencijalne funkcije imamo bezdimenzionu veličinu baš kako i treba.

Postavlja se pitanje prirode operatora koji je tendenciozno označen sa . Za ovo nam treba jednačina za evoluciju fizičkih veličina tj. opservabli. Iz linearne algebre znamo da ako u vektorskom prostoru deluje transformacija operatorom u operatorskom prostoru nad datim vektorskim prostorom deluje transformacije gde je iz operatorskog prostora. Pošto evolucioni operator deluje u vektorskom prostoru na gorepomenuti način u operatorskom će delovati tako što će neki operator (opservablu) evoluirati iz nekog početnog trenutka u trenutak t na sledeći način . Ako razmotrimo infinitezimalnu evoluciju imaćemo . Leva strana je , a desna je . Na desnoj strani je korišćen razvoj eksponencijalne funkcije koja u parametru ima malo dt. Sređivanjem desne strane se dobija da je ona . Izjednačavanjem ovoga sa levom stranom i skraćivanjem se dobija rezulatat . U klasičnoj mehanici za fizičke veličine koje ne zavise eksplicitno od vremena važi nešto slično gde uglaste zagrade označavaju poasonove zagrade, a H je hamiltonijan. Ako se sada vratimo na postulat o kvantizaciji koji daje preskripciju za prelaz sa klasične na kvantnu mehaniku koji kaže da odgovarajuća varijabla prelazi u opservablu i da poasonove zagrade prelaze u komutator pomnožen sa vidimo da operator odgovara hamiltonijanu sistemu.

Eto, to je bio manje-više „pokaz“ dobijanja Šredingerove jednačine. Rigorozan dokaz ima isti koncept, ali je mnogo detaljniji. Imaš sve detalje u Herbutovoj knjizi iz QM ako si voljan da čitaš.

" Plankov rad iz 1901"
Herbutovoj knjizi iz QM
daj linkove da je skinemo ako je ima besplatno na netu.

Fedor Herbut - Kvantna Mehanika.
Engleski prevod plankovog rada

Koji program otvar ps file-ove

Npr. Adobe Distiller, a verovatno i Alladin Ghost. Distiller je u paketu sa Adobe Acrobat-om (me Acrobat Reader-om). Za vikend idem kuci pa cu moci da uploadujem pdf ako ne uradis nista.

_{[Ovu poruku je menjao tomkeus dana 11.07.2007. u 17:36 GMT+1]}

Ne ide mi . Moze pdf

Evo knjige u pdf-u.

Fedor Herbut - Kvantna Mehanika

Jedna napomena: Ova knjiga je napisana za kurs kvantne mehanike na B-smeru Fizičkog Fakulteta u BG-u. Taj kurs nije baš standardan i ume da bude prilično matematički intenzivan. Sama knjiga je pisana matematičkim stilom. Polazi se od malog broja aksioma i potom se izvode njihove posledice. Takođe se podrazumeva da su studenti koji slušaju predavanja prošli kroz kurseve Matematička Fizika I i II. Ovi kursevi se predaju po sledećim knjigama:

Ivanka Milošević - Vektorski prostori i elementi vektorske analize
Milan Damnjanović - Hilbertovi prostori i grupe

Nema nikakvih problema sto se tumacenja tice. Hvala na trudu. Sad cu malo da citam.