• Naslovna
• FAQ
• Pravilnik
• O ES-u
• Tim
• Korisnici
• Statistike

 

• elitesecurity ::
• elitemadzone ::
• EMAIL ::
• RSS ::
• ES Mobile

  Niste ulogovani?  Username :   Password:   

• Registracija
• Zaboravili ste password?
• Flashback ▲▼
• Login problem?

 

Pretraga:

 

Srodne teme 05.07.2003. zadatak - analiticka geometrija 01.07.2004. Matematicka Indkucija / Binomni obrazac 31.05.2004. linearni operatori 13.12.2004. Analiticka Geometrija presjek dvije prave? 30.01.2005. zadatak-analiticka geometrija 30.03.2008. knjiga linearna algebra i analitička geometrija 02.04.2005. zadatak- analiticka geometrija 03.01.2007. Samsung CW 29 M 064 N poremecena geometrija??? 22.03.2007. zadaci, analiticka geometrija 12.05.2007. Analiticka geometrija u ravni Navigacija Brisanje liste Aktuelne teme u ovom forumu: Još jedan zadatak sa uglovima Treći zadatak sa uglovima Ostala rešenja algebarske jednačine Lep zadatak sa uglovima Najmanje pozitivno realno r Ikosaedar i gustina ms matematika.... Jedan zadatak sa pravouglim trouglom Japanese | Can you solve this ? | Math.. Jednakostraničan trougao Logaritamska nejednakost Raspoređivanje slova Košarkaši lep zadatak Zanimljiv zadatak o uglovima trougla Stado Boga Sunca ... 2000 godina star .. Izaberite forum: Linux Linux aplikacije Linux desktop okruženja Linux hardware Windows desktop Windows aplikacije Zaštita Office Windows drajveri Office :: Word Office :: Excel Macintosh Mac hardware Mac software Iphone Enterprise Networking SOHO Networking Wireless Windows mreže Linux mreže Wireless :: WiMax Wireless :: Mikrotik Wireless :: Wireless oprema Linux/UNIX serveri i servisi Unix BSD Skript jezici Security Virtualizacija Cloud Computing Services Security :: Kriptografija i enkripcija .NET 3D programiranje Art of Programming Asembler C/C++ programiranje Kernel i OS programiranje Pascal / Delphi / Kylix Java Embedded sistemi Perl PHP Python Visual Basic 6 Veštačka inteligencija Security Coding XML GameDev - Razvoj Igara Ostali programski jezici PHP :: PHP za početnike PHP :: Smarty template engine .NET :: .NET Desktop razvoj .NET :: ASP.NET .NET :: WPF Programiranje C/C++ programiranje :: C/C++ za početnike Baze podataka MySQL Oracle Access MS SQL Firebird/Interbase PostgreSQL Fiksna telefonija VoIP Udruženje korisnika teleko.. GSM - telefoni GSM - upotreba GSM - servisiranje Mreže i novosti Smartphone Mreže i novosti :: Mobilni internet Mreže i novosti :: Telenor - korisnički servis Mreže i novosti :: VIP - korisnički servis Mreže i novosti :: MTS - korisnički servis Smartphone :: Symbian OS Smartphone :: Windows Mobile Smartphone :: Android GSM - telefoni :: Nokia PDA Uređaji GPS Portable Players Anonimnost i privatnost ISP Browseri E-mail Instant Messaging FTP Google Hosting ISP :: Wireless mreže i ISP ISP :: ADSL E-mail :: Anti-spam Instant Messaging :: IRC Hosting :: Domeni Google :: Gmail E-Marketing Web aplikacije Web dizajn i CSS Web dizajn softver Web razvoj Pretraživači i SEO Flash Javascript i AJAX Web dizajn i CSS :: Kritike Grafički dizajn Izdavaštvo 3D modelovanje Rasterska grafika Vektorska grafika 3D modelovanje :: CAD/CAM Matične ploče, procesori .. Video karte i monitori Storage Ostali hardver Overclocking & Modding PC Konfiguracije Laptopovi Vodič za kupovinu - PC har.. Tablet PC Muzička produkcija Audio kompresija Audio softver Video produkcija Video kompresija Video softver Multimedijalni uređaji Digitalni fotoaparati Digitalne kamere Home Theater Digitalni fotoaparati :: Fotografija Digitalni fotoaparati :: Vodič za kupovinu - Digita.. Elektronika Elektrotehnika Elektronika :: TV uređaji Elektronika :: Radio elektronika i tehnika Elektronika :: Mikrokontroleri Elektronika :: Audio-elektronika Auto-elektronika :: Tuning Vodič za učenje Vodič za posao Vodič za emigraciju Fizika Matematika Nauka Sertifikati Informatika Vodič za učenje :: Seminarski radovi Vodič za učenje :: Obrazovne institucije Vodič za emigraciju :: Život u USA Vodič za emigraciju :: Život u Norveškoj Vodič za emigraciju :: Život u Nemačkoj E-Poslovanje E-Kupovina IT pravo i politika razvoja IT događaji IT berza poslova IS i ERP Ekonomija Berza Cryptocoins IT berza poslova :: Arhiva IT berze poslova IT pravo i politika razvoja :: Registar Nacionalnog ID E-Poslovanje :: E-Transakcije E-Poslovanje :: Forex E-Kupovina :: Platne kartice Digitalna Televizija Advocacy Ankete Predlozi i pitanja Vesti Čekaonica Vesti :: ES leto manifestacija MadZone TechZone Poljoprivreda AutoZone MotoZone Svakodnevnica Video igre MadZone :: Zanimljivi linkovi MadZone :: Kultura TechZone :: Ergonomija TechZone :: Grejanje TechZone :: Klimatizacija TechZone :: Bela tehnika AutoZone :: Fiat Panda club Lista poslednjih: 16, 32, 64, 128 poruka.

darkosos Darko Šoš Beograd Član broj: 5053 Poruke: 1131 95.180.54.* +64 Profil Re: Analiticka geometrija problem 15.05.2012. u 17:53 - pre 157 meseci Probaj ovako: izracunaj rastojanje od centra kruga do sredista tetive duzine 10 (ovaj deo prakticno nije analiticka geometrija). Ako nadjes krug koncentrican datom, sa tim rastojanjem kao poluprecnikom, svaka tangenta na taj krug odseca tetivu duzine 10 na vecem krugu. Ostaje da se jos, dakle, nadje tangenta na taj krug iz tacke A. Odgovor na temu

smorilasamse ne radim srbija Član broj: 306508 Poruke: 32 *.static.madnet.rs. +1 Profil Re: Analiticka geometrija problem 21.09.2012. u 11:31 - pre 153 meseci http://i49.tinypic.com/35bihix.png posto mi je data osa Oy, da li cu je zapisati kao x=0? drugi deo zadatka mi je jasan.. (vektor prave je u stvari vektorski proizvod vektora prave q i vektora ravni alfa) Odgovor na temu

darkosos Darko Šoš Beograd Član broj: 5053 Poruke: 1131 *.static.isp.telekom.rs. +64 Profil Re: Analiticka geometrija problem 21.09.2012. u 11:58 - pre 153 meseci Posto si u 3D, treba i z=0. Mislim, to je ono ocigledno, presek je y=-4. Takodje, jednacine x=0 i z=0 su jednacine ravni, pa njihov sistem zaista predstavlja jednacinu prave, y-ose. Slicno nacinu na koji je zadata druga prava u zadatku. Naravno, to je vise teorijska primedba, jer i malo dete moze u jednacinu ravni da stavi da su x i z jednaki 0 :) Odgovor na temu

smorilasamse ne radim srbija Član broj: 306508 Poruke: 32 *.static.madnet.rs. +1 Profil Re: Analiticka geometrija problem 21.09.2012. u 12:22 - pre 153 meseci je,nikako da se otarasim analitike u ravni i da se preselim na prostor.. jos jedno pitanje.. znam da dve prave koje se seku obrazuju ravan.. a da li dve paralelne prave obrazuuju ravan.. ja sam mislila da ne... pa sam onda procitala ovo :http://i47.tinypic.com/31359us.png Odgovor na temu

smorilasamse ne radim srbija Član broj: 306508 Poruke: 32 *.static.madnet.rs. +1 Profil Re: Analiticka geometrija problem 21.09.2012. u 12:30 - pre 153 meseci http://i49.tinypic.com/2s7f0xu.png konkretan zadatak,pod b.. kako da dobijem vektor ravni.. dobijam uvek (0,0,0) Odgovor na temu

darkosos Darko Šoš Beograd Član broj: 5053 Poruke: 1131 *.static.isp.telekom.rs. +64 Profil Re: Analiticka geometrija problem 21.09.2012. u 12:33 - pre 153 meseci Ne znam kako da ti odgovorim na ovo, to je pitanje geometrijske intuicije... Zamislis dve paralelne prave (u prostoru).... probas da zamislis neku ravan koja ih sadrzi... razmislis da li je ta ravan jedinstvena... I voila! Naravno, mozes i da odlucis da verujes izvoru koji to izvodi dedukcijom... Odgovor na temu

smorilasamse ne radim srbija Član broj: 306508 Poruke: 32 *.static.madnet.rs. +1 Profil Re: Analiticka geometrija problem 21.09.2012. u 12:40 - pre 153 meseci usvojicu to.. al sta da napisem profesoru kao odgovor.. jednacina ravni γ : 0=0 ??? Odgovor na temu

darkosos Darko Šoš Beograd Član broj: 5053 Poruke: 1131 *.static.isp.telekom.rs. +64 Profil Re: Analiticka geometrija problem 21.09.2012. u 12:42 - pre 153 meseci Ono je bio odgovor na prethodno pitanje... Sto se tice zadatka, verovatno su prave paralelne... Probaj da izaberes drugacije vektore za vektorski proizvod... Odgovor na temu

smorilasamse ne radim srbija Član broj: 306508 Poruke: 32 *.static.madnet.rs. +1 Profil Re: Analiticka geometrija problem 21.09.2012. u 12:46 - pre 153 meseci ne mogu da izaberem druge,jer mi je receno da za m uzmem da je m=2 Odgovor na temu

darkosos Darko Šoš Beograd Član broj: 5053 Poruke: 1131 *.static.isp.telekom.rs. +64 Profil Re: Analiticka geometrija problem 21.09.2012. u 12:48 - pre 153 meseci Uh... Jesi li ti to na ispitu? U svakom slucaju, posto verovatno mnozis vektore pravca pravih p i q, ako su paralelne, dobijas 0. Zato uzmes p i vektor npr. AP za bilo koje P sa prave p... Odgovor na temu

smorilasamse ne radim srbija Član broj: 306508 Poruke: 32 *.static.madnet.rs. +1 Profil Re: Analiticka geometrija problem 21.09.2012. u 12:52 - pre 153 meseci nisam ,ali bicu sutra :D Odgovor na temu

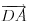
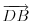
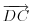
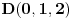
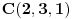
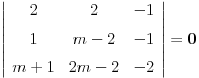
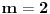
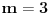
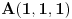
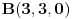
Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.3gnet.mts.telekom.rs. +2801 Profil Re: Analiticka geometrija problem 21.09.2012. u 13:56 - pre 153 meseci Nađi dve tačke C i D koje pripadaju pravoj p, a onda postavi uslov da su vektori , i linearno zavisni. Recimo za i dobija se jednačina čija su rešenja i . Neka je sada m=2. Tačke A i B imaju koordinate i . 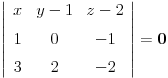Ravan koja prolazi kroz tačke A, B i D ima jednačinu odnosno . 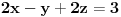Rastojanje tačke A od prave p=CD je . 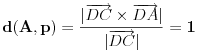Dakle, jednačina kružnog cilindra sa osom p koji sadrži tačku A glasi . 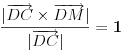Naravno, može se koristiti poznata formula . 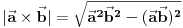Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.3gnet.mts.telekom.rs. +2801 Profil Re: Analiticka geometrija problem 21.09.2012. u 22:49 - pre 153 meseci U jednačini cilindra je naravno . Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

smorilasamse ne radim srbija Član broj: 306508 Poruke: 32 *.static.madnet.rs. +1 Profil Re: Analiticka geometrija problem 22.01.2013. u 09:51 - pre 149 meseci Dati su jedinicni vektori a=OA, b=OB , c=OC koji obrazuju triedar desne orijentacije, takvi da a normalno na b , b normalno na c ,c normano na a. Izraziti vektor AD preko datih vektora , gde je D ortogonalna projekcija tacke A na pravu BC . Molim vas,prosvetlite me.. Nas asistent nije znao da nam uradi ovaj zadatak,a redovno se pojavljuje na ispitu .. Odgovor na temu

darkosos Darko Šoš Beograd Član broj: 5053 Poruke: 1131 *.static.isp.telekom.rs. +64 Profil Re: Analiticka geometrija problem 22.01.2013. u 10:49 - pre 149 meseci OD = 1/2 (OB+OC) => AD = AO+OD = -OA + 1/2 (OB+OC), mozda? a, b i c kao da su na osama pravouglog koordinatnog sistema... a da je D na sredini duzi BC bi trebalo da sledi iz teoreme o tri normale... Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.3gnet.mts.telekom.rs. +2801 Profil Re: Analiticka geometrija problem 22.01.2013. u 11:42 - pre 149 meseci Neka je . , . Dakle, , , odakle sledi . Uzimajući u obzir da je i , dobijamo da je , odnosno . Dakle, . Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

darkosos Darko Šoš Beograd Član broj: 5053 Poruke: 1131 *.static.isp.telekom.rs. +64 Profil Re: Analiticka geometrija problem 22.01.2013. u 13:53 - pre 149 meseci Znaci, to je to... Onda da malo pojasnim prethodnu moju poruku... Teorema o tri normale nam daje da se podnozje normale iz A na BC poklapa sa podnozjem normale iz O na BC. Posto je trougao OBC jednakokraki sa |OB|=|OC|, podnozje normale iz O na BC je srediste duzi BC. Dakle, OD je polovina dijagonale romba koju obrazuju vektori OB i OC. Ostalo je lako, kao sto sam i napisao. Mislim jos da ovo vazi i pri slabijim uslovima: dovoljno je da je OA normalno i na OB i OC, i da je |OB|=|OC|. Dakle, nijedan vektor ne mora biti jedinicni, a ne moraju biti ni uzajamno normalni OB i OC ... Nije mi jasno kako ovakav zadatak asistent nije znao da resi? Mozda sam pogresno nesto razumeo... Odgovor na temu

smorilasamse ne radim srbija Član broj: 306508 Poruke: 32 *.static.madnet.rs. +1 Profil Re: Analiticka geometrija problem 22.01.2013. u 18:57 - pre 149 meseci mozda nije namerno hteo da nam resi kad smo ga pitali,da bismo se mucili na ispitu.. ko zna. Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.3gnet.mts.telekom.rs. +2801 Profil Re: Analiticka geometrija problem 22.01.2013. u 19:11 - pre 149 meseci Smisao ispita nije mučenje, već provera znanja. Takođe, ni smisao vežbi nije mučenje na ispitu, već sticanje znanja. Poenta je upravo u tome da na nastavi (čiji oblici uključuju i predavanja i vežbe i konsultacije) nešto naučite i da posle položite ispit. Naravno, oni koji su naučili to što je predavano. Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.3gnet.mts.telekom.rs. +2801 Profil Re: Analiticka geometrija problem 22.01.2013. u 20:28 - pre 149 meseci A ko je asistent? Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu