Ako misliš na slučaj sa
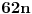
, on može da se dokaže primenom matematičke indukcije. Možda može i na jednostavniji način, ali ovo je jedino što mi za sada pada na pamet.
1) prvo se dokaže da je iskaz zadovoljen za

:
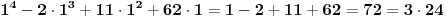
2) zatim se dokazuje da, ako je iskaz tačan za neko

, biće tačan i za

:
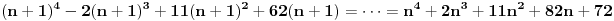
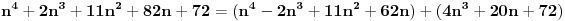
Pošto je izraz u prvoj zagradi po pretpostavci deljiv sa
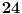
, treba dokazati da je izraz u drugoj zagradi,
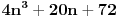
takođe deljiv sa
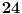
. Pošto je
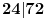
, to dokazivanje se svodi na dokazivanje da je
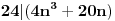
.
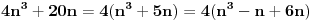
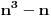
je deljivo sa
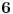
za svako

, samim tim će i
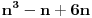
biti deljivo sa
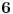
za svako

.
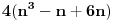
je, prema tome, deljivo sa
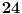
za svako

.