Vecina funkcija u fizici se relativno dobro ponasaju. Matematicki, to znaci da imaju sve izvode u okolini koja nas zanima. U suprotnom mora da postoji neki fizicki razlog za nepostojanje k-tog izvoda sto takodje onemogucava pisanje Taylorovog reda.
Nazalost, postojanje svih izvoda funkcije jedne realne promenljive nije dovoljan uslov za konvergenciju Taylorovog reda u zadatoj okolini. Primer za to je
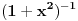
. Ova funkcija ima sve izvode na realnoj osi ali joj Taylorov red oko

konvergira samo u intervalu
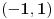
.
Razlog za to je sto zadata funkcija ima polove (singularitete) u kompleksnoj ravni za
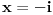
i
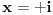
. U stvari, u matematici vazi sledece:
Ako funkcija
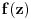
kompleksne promenjljive

ima dobro definisan jedan izvod
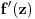
u okolini oblika diska radiusa

tacke
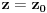
, onda
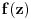
:
1) ima sve izvode u istoj okolini
2) ima Taylorov red za tacku
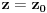
koji konvergira za
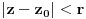
Pitanje konvergencije Taylorovog reda neke fizicke funkcije stoga treba posmatrati kao pitanje ponasanja takozvanog "kompleksnog produzenja" te funkcije. Ovo produzenje dobijamo ako u jednacinama cije je resenje

dozvolimo da

poprimi kompleksne vrednosti i na taj nacin kao resenje dobijemo funkciju kompleksne promenjljive. U vecini fizickih sistema ovakvo produzenje je moguce i cak je *veoma ocigledno*.
Ako se kompleksno resenja dobro ponasa (svugde ima izvod), onda ce i Taylorove ekspanzije realnog resenja biti dobre (konvergirajuce).
Sa druge strane, lose ponasanje "kompleksizovanog" resenja cesto je indikacija nekog zanimljivog fizickog fenomena.
Sve u svemu moj odgovor je u nekoj meri filozofski:
Generalno ne treba pretpostavljati da realne fizicke funkcije imaju validne Taylorove redove (iako je to cesto slucaj). Umesto toga, treba razmotriti ponasanje "kompleksno produzenog" fizickog sistema. Ako se taj sistem dobro ponasa, konvergencija Taylorovog reda je matematicki zagarantovana. Ako ne, razlog je najverovatnije pravi fizicki fenomen koji je iz ponasanja realnog resenja mnogo manje ocigledan.
Marko