Ok, ide ovako:
Mozemo se ograniciti na konacne skupove tacaka. :)
Prvo neka je

, neki skup razlicitih tacaka (
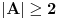
) i
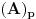
skup svih pravih koje su odredjenje elementima skupa

(jel ovako ok? :)). Skup

ima svojstvo
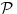
, ako nisu sve tacke iz tog skupa kolinearne.
Dokazac1emo obicnom indukcijom po
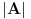
da je
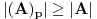
, za svaki skup

koji poseduje svojstvo
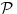
(izostavicemo slucajeve
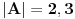
, jer su trivijalni).
baza indukcije: Za
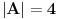
. Prostom analizom slucajeva vidimo da vazi data nejednakost. :)
ind. pretpostavka: Neka za svaki skup tacaka

koji ima
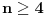
elemenata i poseduje svojstvo
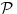
vazhi data nejednakost.
ind. korak: Dokazimo da sada za svaki skup tacaka

koji ima

element i poseduje svojstvo
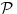
vazi data nejednakost.
U tom slucaju mozemo iz skupa

mozemo izdvojiti podskup koji ima

elemenata i poseduje svojstvo
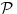
(u suprotnom bi svakih

tacaka iz toga skupa lezale na jednoj pravoj, pa bi i sve tacke skupa

lezale na jednoj pravoj zbog
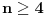
, sto bi bila kontradikcija). Neka je ostala tacka

posle izdvajanja skupa od

tacaka sa svojstvom
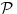
iz skupa

. Po induktivnoj pretpostavci je
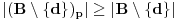
. Sada je dovoljno dokazati da tacka

sa nekom od preostalih tacaka obrazuje pravu koja nije element
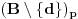
. Pretpostavimo suportno tj. da svaki element skupa
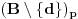
sadrzhi tacku

. Kako je
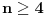
to je
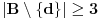
, pa postoje tri nekolinearne tacke iz skupa
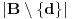
. Neka su to
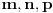
. Po pretpostavci vazhi da prave
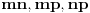
sadrze tacku

, pa se one seku u jednoj tacki. Ovo je kontradikcija jer te prave sadrze stranice trougla
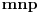
(svojstvo
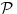
).
Znaci bar jedan od elemenata skupa
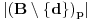
ne sadrzi

, pa vazhi
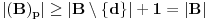
.
Ovim je dato tvrdjenje dokazano.
 prirodan broj takav da je
prirodan broj takav da je 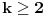 . Koliko najvise tacaka u ravni moze da obrazuje ukupno
. Koliko najvise tacaka u ravni moze da obrazuje ukupno  pravih?
pravih?