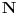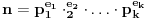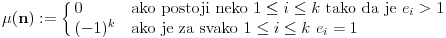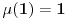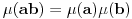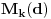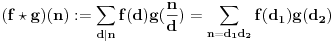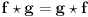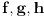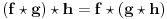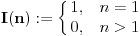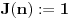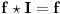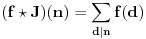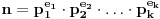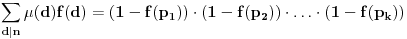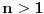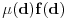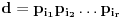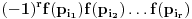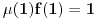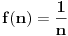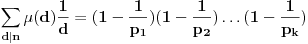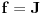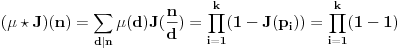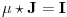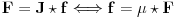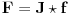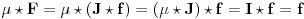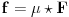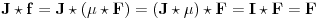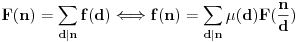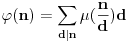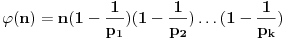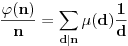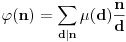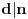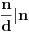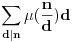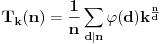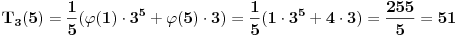Möbius-ova funkcija se definiše na skupu
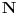
na sledeći način:
Neka je
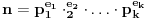
faktorizacija broja

na proste ÄŤinioce, onda je
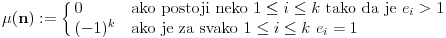
Specijalno, uzima se da je
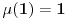
.
Drugim reÄŤima,

f-ja je jednaka nuli za one brojeve koji su deljivi kvadratom nekog broja (većeg od 1), a za brojeve koji su jednaki proizvodu recimo

razliÄŤitih prostih brojeva je jednaka

ili

u zavisnosti od parnosti broja

.
OÄŤigledno je da je

multiplikativna f-ja jer pored već pomenutog
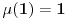
vaĹľi i
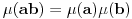
kad god su

i

uzajamno prosti.
Najčešće korišćena teorema u vezi sa ovom f-jom je tzv.
Möbius-ova formula inverzije (koju si ti? i upotrebio kada si računao
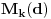
).
Dirichlet-ov proizvod dve aritmetiÄŤke f-je (to su one ÄŤiji je domen
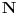
a kodomen
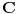
) se definiše sa:
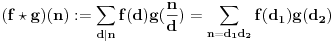
OÄŤigledno je da vaĹľi
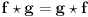
.
Lako je pokazati da je ovako definisan proizvod aritmetiÄŤkih f-ja asocijativan tj. da za proizvoljne aritm. f-je
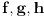
vaĹľi
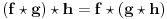
Pre nego što dođemo do formulacije
Möbius-ove formule inverzije i njenog dokaza pogledajmo još dve f-je:
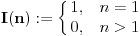
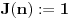
Jasno je da su obe f-je multiplikativne.
Na osnovu definicija odmah sledi da za svaku aritm. f-ju

vaĹľi:
1. 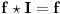 2.
2. 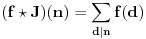 Lema
Lema
Ako je

multiplikativna f-ja i ako je
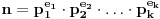
faktorizacija broja

na proste ÄŤinioce, onda vaĹľi:
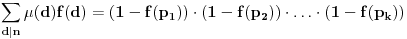
Dokaz.
Ako je

desna strana se (kao što je za proizvode i uobičajeno) tumači kao 1 pa jednakost važi.
Ako je
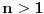
, na osnovu definicije
Möbius-ove f-je, jasno je da će se u sumi efektivno pojavljivati samo članovi
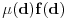
kod kojih je
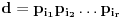
tj. ÄŤlanovi oblika
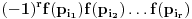
pa je suma (uzmemo li u obzir
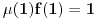
) upravo jednaka desnoj strani jednakosti zapisanoj u razvijenom obliku.
Specijalno, ako stavimo da je
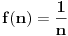
(multiplikativnost je oÄŤigledna) dobijamo da je
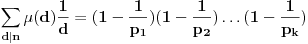
.
Još jedan važan primer dobijamo ako stavimo
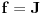
.
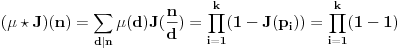
Dakle, dobili smo da vaĹľi
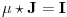
.
Najzad:
Teorema (
Möbius-ova formula inverzije)
Ako su

i

aritmetiÄŤke f-je, onda vaĹľi:
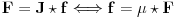
.
Dokaz.
Ako je
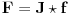
, onda posle mnoĹľenja te jednakosti sleva f-jom

, dobijamo
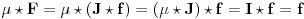
.
Obrnuto, ako je
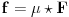
, onda posle mnoĹľenja te jednakosti sleva f-jom

, dobijamo
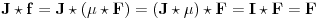
Ako se prisetimo kako je definisana operacija

vidimo da se ova teorema moĹľe iskazati i ovako:
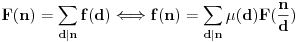
Ostaje da obrazložimo još jedan argument korišćen u tvom radu:
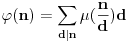
Budući da važi
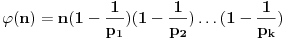
odmah vidimo (na osnovu onog drugog primera u vezi sa
Lemom) da vaĹľi i
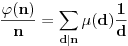
tj.
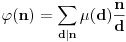
međutim, kad god
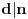
, tada i
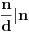
pa je poslednja suma zapravo jednaka sumi
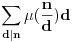
.
Konačno da bi rešio postavljeni zadatak dovoljno je da primeniš
MacMahon-ovu formulu
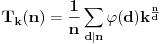
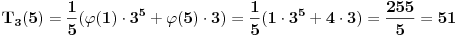
InaÄŤe,
MacMahon je ovaj zadatak rešio 1892. u radu
Application of a theory of permutations in circular procession to the theory of numbers, Proceedings of the London Mathematical Society 23 (1892), 305-313 a jedno od rešenja možeš naći i u knjizi
Concrete mathematics,
R. Graham, D. Knuth, O. Patashnik.
[Ovu poruku je menjao uranium dana 18.05.2006. u 06:52 GMT+1]
Attempt all the problems. Those you can do, don't do. Do the ones you cannot.




 Cikličke permutacije - Möbiusova funkcija
Cikličke permutacije - Möbiusova funkcija