Citat:
miki069:
Da li ga osporavati zbog "formalne" dlake u jajetu.
Sigurno da ne.
Toliko o strogom "formalizmu".
„Dlake o jajetu“ o kojima pričaš mogu, ako se ignorišu, uništiti ceo koncept, kao što je Nedeljko lepo ilustrovao na primeru Poasonove parcijalne diferencijalne jednačine
ovde (na šta je, štaviše, Petar naknadno skrenuo pažnju). Iskreno si nadam da si to pročitao pre nego što si krenuo da iznosiš ovoliko matematički besmislene tvrdnje, ali deluje da si propustio i Nedeljkovu poruku i Petrovo pozivanje na nju.
Sad da se vratimo na primer koji tako trijumfalno potenciraš. Formula
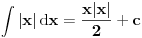
, osim što je „inžinjerski OK“, takođe je tačna. Kažeš da je rezultat integrala funkcija koja nije diferencijalna u svakoj tački. Ma nemoj. Pretpostaviću da misliš na tačku
(ona tu deluje najproblematičnija), i pokazaću da je funkcija u toj tački diferencijalna bez problema:
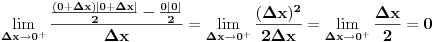
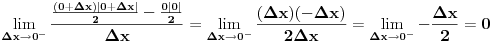
Kako u dotičnoj tački postoje i levi i desni izvod, i pri tom se poklapaju, sledi da je funkcija diferencijalna u toj tački.
Dakle, formula koju si naveo je strogo matematički tačna, i zato je inžinjeri mogu praktično primenjivati. Da je ona, kojim slučajem, matematički pogrešna (bez obzira na to koliko „dlaka u jajetu“ bila sitna), nikakva „praktičnost“ je ne bi mogla spasti. Moram priznati, šokiran sam besmislom izjave da „praktična“ formula (šta god to značilo) ne mora biti matematički tačna. Od koga si uopšte to mogao „naučiti“??
Sada ću pokazati kako si ovim komentarom zapravo potvrdio koliko
ne valja učiti iz Apšena. Eto, mrtav ’ladan si izjavio da je ova formula matematički netačna (!), jer funkcija nema izvod u svakoj tački (!!). Da si učio iz ozbiljne literature, znao bi da su ove dve izjave besmislene (kao što sam gore pokazao) — ali eto, učio si iz Apšena, i sasvim prirodna posledica toga jeste to što ne znaš da proveriš izvod funkcije u nekoj „komplikovanijoj“ tački. Dobro je što su se u ovom primeru matematika i „praktičnost“ poklopile, ali to se neće uvek dogoditi, i tada će ti se zbog preskakanja „dlake u jajetu“ srušiti zgrada (još jednom te upućujem na Nedeljkovu poruku). Zato svaka „praktična“ formula mora, pre svega, biti matematički tačna, a moraš naučiti da to lepo proveriš (kao što sam ja sada proverio tvoju „praktičnu“ formulu, i pokazao da ona jeste matematički tačna).
Zaključak bih na kraju posebno izdvojio, da ne bi nekom ipak promakao: kolega miki069 je na sopstvenom primeru pokazao da onaj ko uči iz Apšena ne zna da izračuna izvod funkcije
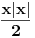
u tački
; štaviše, uveren je da izvod u toj tački ne postoji, ali da to nije bitno za ispravnost formule. To bi trebalo da bude dovoljno ilustrativan zaključak ove teme.
Ljubičice crvena, što si plava kô zelena trava.
Re: Najbolja zbirka iz Matematike I
Registrovani: 4 ( Nedeljko, ackopk, BlackForce, Ultrena )
Npr. miki069 ili igorpet?