Dirichlet-ov proizvod se definiše kao:
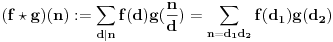
Ako su

i

multiplikativne, onda je i
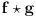
.
Dokaz:
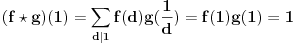
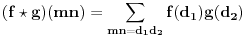
,
pošto su

i

uzajamno prosti, onda za svako
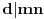
važi:
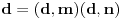
, pa dobijamo:
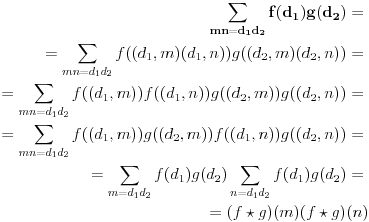
,
Pretposlednja jednakost važi zato što : iz
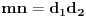
, sledi i
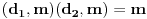
(i analogno
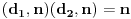
). Dakle, svaka faktorizacija
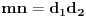
generiše jedinstvene (do na poredak) faktorizacije
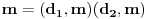
i
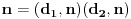
, kao i obrnuto svake dve faktorizacije
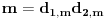
i
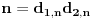
generišu jedinstvenu (do na poredak) faktorizaciju
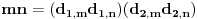
za koju je
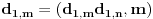
,
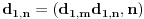
i analogno za
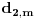
i
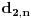
.
Time je dokazano tvrđenje.
Primetimo najzad da je funkcija
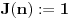
multiplikativna i da je
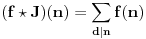
takođe multiplikativna, pod uslovom da je i f takva.
Što se tiče zadatka, sada nije teško pokazati i
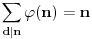
(naravno, sam zadatak se može rešiti i daleko prostije)
[Ovu poruku je menjao uranium dana 01.07.2005. u 08:23 GMT+1]
[Ovu poruku je menjao uranium dana 01.07.2005. u 08:25 GMT+1]
[Ovu poruku je menjao uranium dana 01.07.2005. u 08:35 GMT+1]
Attempt all the problems. Those you can do, don't do. Do the ones you cannot.