Evo, da dopunim onaj moj prethodni post.
Prvo, obrazloženje zašto uopšte posmatramo onu relaciju

i politope. Izaberimo bilo koje
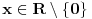
. Posmatrajmo sada sve skupove od po

brojeva na koje će definisanje broja

imati uticaja:
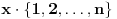
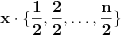

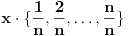
.
Jasno je da se svaki od ovih skupova može dobiti multiplikativnom translacijom bilo kog drugog navedenog skupa. Ali sada moramo da definišemo f-ju i u svim preostalim navedenim tačkama, što nas opet vraća na generisanje novih

-torki (koje se opet mogu dobiti translacijom ovih postojećih). A za samu translaciju dovoljno je da množimo (odnosno delimo) samo sa prostim brojevima ne većim od

.
Neka je

prost broj i neka je kao i obično
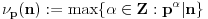
f-ja definisana na
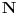
.
Ako uzmemo kao u mom prethodnom postu da je
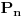
skup prvih
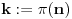
prostih brojeva, onda definišimo multiplikativnu grupu generisanu skupom
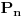
tj. neka je
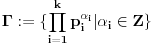
.
Sada primetimo da prilikom svake translacije politopa
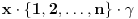
(pri čemu je
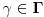
) "za" broj
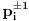
dobijamo novi politop koji će imati zajedničkih temena sa prethodnim, ali će (a to je bitnije) imati i barem jedno novo teme. Evo barem jednog novog temena: neka je
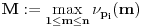
neka je
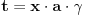
teme politopa kod koga je
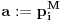
ako je translirano za
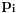
odnosno
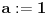
ako se radi o translaciji za
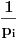
. Lako je videti da za celo
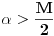
translati za
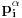
i
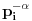
nemaju zajedničkih temena. A u slučaju kada je
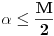
onda pomenuti translati imaju barem po jedno teme koje se nije "pojavilo" ni u jednom translatu za
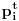
gde je
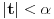
i
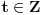
.
Dakle, nakon inicijalnog definisanja f-je u temenima osnovnog politopa, svaka njegova elementarna translacija imaće neprazan skup novih temena pa ćemo moći da f-ju dodefinišemo u njima tako da f-ja zadovolji traženi uslov na translatu.
Najzad smo spremni da krenemo na glavni deo.
Potreban nam je neki algoritam koji će nam translacijom "prošetati" osnovni politop
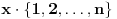
po svim preostalim politopima (sa temenima iz iste klase ekvivalencije) ali tako da preko svakog pređemo
tačno jednom.
Neka je operator
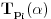
translacija za
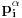
(
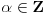
) i neka je
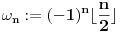
. Od sada pa na dalje za "kretanje" po hiperprostoru koristićemo nizove pomenutih translacija:
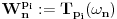
. Znači prvih
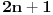
vrednosti za
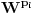
biće
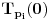
,
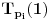
,
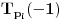
,
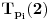
,
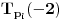
,

,
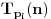
,
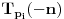
.
Ideja je da definisanje f-je izvršimo induktivno, i sada bi ovde lepo legla priča preko ordinala i afinih potprostora, koju ću ja pokušati da formalno (ali ne i suštinski

) izbegnem.
Već smo uočili da svaki politop možemo predstaviti u obliku,
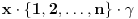
, pri čemu je
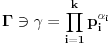
. Dakle, broju
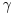
odgovaraju koordinate
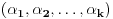
. Da bismo pratili "kretanje" politopa
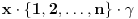
dovoljno je da pratimo koordinate broja
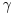
. Evo kojim redom će se vršiti dodefinisanje:
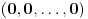
,
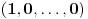
,
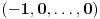
,
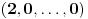
,
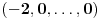
...
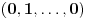
,
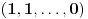
,
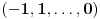
,
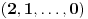
,
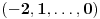
...
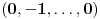
,
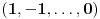
,
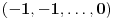
,
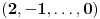
,
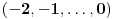
...
Dakle, u prvom koraku držimo fiksirane koordinate
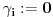
(
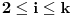
) a za svako
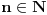
šetamo
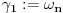
. Kada to završimo (joj šta bi
Kroneker rek'o za ovo

) onda stavimo da je
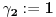
i
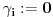
za
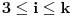
a opet prošetamo
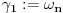
za svako
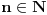
. Zatim, stavimo da je
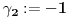
i
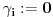
za
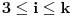
a opet prošetamo
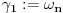
itd.
Mislim da je jasna šema: ako je izvršeno potpuno definisanje f-je za politope kod kojih je
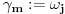
za sve
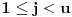
i
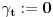
za
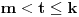
onda definišemo f-ju (rekurentno po dužini
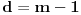
početnog dela

-torke) i u svakom politopu kod koga je
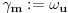
i
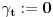
za
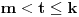
.
Da zaključimo: za sve je kriv
Farenhajt 
da me nije prozvao - ne bih nikog ni mučio sa ovako "elegantnim" idejama

Attempt all the problems. Those you can do, don't do. Do the ones you cannot.
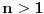 . Da li postoji funkcija
. Da li postoji funkcija 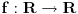 takva da je
takva da je 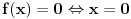 i
i 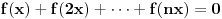 za svako
za svako  ?
?