Da moze! Tu i bas nema velike teorije, mnoge stvari mozes i sam da provalis. Nazalost tvoje trenutno znanje nema velike veze sa takmicarskim zadacima. Sto se tice teorije grafova ona se pada tek na saveznom takmicenju, tako da ti je najbitnije u pocetku na naucis dinamicko programiranje. Kao sto reko, tu nemas teoriju vec je to samo jedan princip gde neko resenje svodis na trazenje manjih resenja. Npr. evo jednog banalnog primer:
Data je matrica
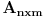
popunjena celim brojevima. Patuljak krece iz gornjeg levog ugla i treba stici u donje desno polje, ali tako da je ukupan zbir brojeva u poljima na koje stane patuljak maximalan. Patuljak moze da se krece na dole ili u desno.
Normalno, ovde da generises sve moguce puteve je stvarno glupo, jer broj tih puteva raste eksponencionalnom brzinom. E zato cemo probati da problem najveceg zbira matrice NxM svesti na neke manje matrice od nje, pa sasvim logicno dobijas da je najveci zbir od polja (1,1) do polja (N,M) jednak:
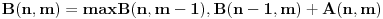
,
jer ti u polje (n,m) mozes doci samo reko polja (n,m-1) i polja (n-1,m) i naravno toj sumi dodas broj u polju (n,m)...
Pored dinamickog programiranja, traba na naucis neke koriste "algoritme" tipa: Binarna pretraga, QuickSort, Heap, LIS, LCS... Zatim tu imas i geometriju gde imas: Konveksi omotac, Point in Poly, Dve najblice tacke, Dve naudaljenije tacke...
Literatura:
[1] "Dinamicko programiranje", Milan Vugdelija
[2] "Algoritmi", Miodrag Zivkovic
[3] "Introduction to Algotirhms", Udi Manber
[4] i naravno da provezbas poslednjih 10-ak godina
Takodje preporucio bi na radis zadatke na online testeru USACO! Tamo je sve to postupno i odradjeno i objasnjeno tako da je za pocetnike super napravljeno...
Math is like love. A simple idea but it can get complicated.