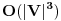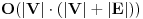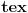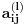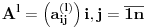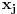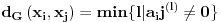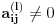Citat:
MrLimeni: Ovaj algoritam(ne ovaj koji je iskucan nego ovaj koji je opisan) se zaustavlja cim se doce do trazenog cvora takoda ne trazi rastojanje do sledecih cvorova.
evo pogledajte ove slajdove sto sam prikacio uz poruku.
Koliko sam ja ukapirao, ti pricas o Floyd-Warshallovom algoritmu, a na ovom slajdu je prikazan BFS. Procitaj moj prethodni post i bice ti sve jasno:
Citat:
IsrkiboyI: Btw,
Floyd-Warshall-ov algoritam sluzi za nalazenje najkracih puteva u bilo kom (dakle i tezinskom) grafu, i slozenosti je
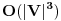
. Ako graf nije tezinski (dakle sve ivice imaju istu tezinu), najkraci putevi se mogu naci i BFS-om, pri cemu bi morao da se pusti BFS iz svakog cvora, pa bi konacna slozenost bila
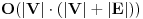
, sto je u opstem slucaju isto kao Floyd-Warshall. Moze se i pustiti i
Dijkstra iz svakog cvora.
Dakle, ono sto je prikazano na pps prezentaciji je BFS iz jednog cvora, sto ce naci najkraca rastojanja od njega do svih ostalih. Ako hoces i ostala rastojanja, markiras sve cvorove kao neprodjene, pa pustis BFS iz B, pa iz C, itd...
Citat:
Teorema: Graf G je bipartitan akko ne sadrži neparne cikluse.
Da! Dokaz:
(=>) Trivijalno. Neka je graf G bipartitan sa biparticijom (A, B). Podjimo od nekog cvora a iz A. Svaki put neparne duzine dovodi nas do cvora u B, a svaki put parne do cvora u A. Kako treba da se vratimo u a da bi napravili ciklus, on mora biti parne duzine.
(<=) Nesto tezi smer. Nadjimo neko drvo razapinjanja u grafu G, i oznacimo ga sa T. Uzmemo neki, bilo koji cvor, v. Do svakog cvora mozemo iz v stici na jedinstven nacin iduci ivicama koje se nalaze u T. Sada tvrdimo da su one do kojih je put parne duzine u jednoj, a do kojih je neparne u drugoj particiji. Za svaku ivicu e (x, y) vazi jedno od sledeca 2:
(i) e se nalazi u T. U ovom slucaju je ili x pretposlednju cvor na v-y putu kroz T, ili je y pretposlednji cvor na v-x putu kroz T. U svakom slucaju duzine puteva do x i y su razlicite, pa su oni u razlicitim particijama.
(ii) e se ne nalazi u T. U ovom slucaju, x-y put u T, zajedno sa ivicom e pravi ciklus. Po
(i) imamo da su cvorovi na x-y putu u T naizmenicno u jednoj i drugoj particiji. Posto je svaki ciklus paran, onda su x i y u razlicitim particijama.
QED
Inace, za proveru da li je graf bipartitan moze se koristiti obican DFS sa markiranjem cvorova crno-belo.
I HAD A NIGHTMARE
IT ALL STARTED NORMAL
10101010
10110011
THEN ALL OF A SUDDEN
1100102
GAAAAH
_____________________________
www.princeton.edu/~skrstic
www.niwifi.co.sr
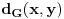 (rastojanje).
(rastojanje).



 Teorija grafova. Implementacija algoritama. HELP :)
Teorija grafova. Implementacija algoritama. HELP :) Re: Teorija grafova. Implementacija algoritama. HELP :)
Re: Teorija grafova. Implementacija algoritama. HELP :) Re: Teorija grafova. Implementacija algoritama. HELP :)
Re: Teorija grafova. Implementacija algoritama. HELP :)