Srodne teme

26.03.2002. definicija
05.05.2003. Condition funkcije u Windows-u ?
14.03.2004. ExtraNet pojam i definicija ???
29.09.2004. brisanje odredjenih definicija?
02.10.2004. Kako naci redosled kojim su pozivane funkcije?
19.09.2005. Definisanje funkcija..... etc?
04.11.2005. Implicitno pozivanje ReleaseMutex funkcije
17.11.2005. Potrebna pomoc oko minimuma funkcije
24.11.2005. Pomoc kod izvodjenja relacije
13.03.2006. Dvije funkcije ;-)

Navigacija

Brisanje liste

Lista poslednjih: 16, 32, 64, 128 poruka.

Definicija funkcije

[es] :: Matematika :: Definicija funkcije

Strane: 1 2

[ Pregleda: 10540 | Odgovora: 23 ] > FB > Twit

Autor

sMRDo
560012548
Graz

Član broj: 56428
Poruke: 63
*.vc-graz.ac.at.

Profil

Definicija funkcije

^{10.05.2005. u 03:40 - pre 243 meseci}

Posmatrajuci funkciju x(x-1)(x-2)/x^2-4 ustanovio sam da funkcija ne moze biti definisana na mjestima -2 i 2. Naime, kako je moguce da mi program za crtanje grafova iscrtava funkciju na 2 koja tu iznosi 0.5??? Kada se izracuna limes za x jednako 2 dobija se upravo ta vrijednost. Kako je moguce da je 0/0 nesto definisano i da je to upravo 0.5. Molim strucnjake za funkcije da podjele znanje sa mnom. Hvala unaprijed.

Odgovor na temu

peddja_stankovic
predrag stankovic
private
beograd

Član broj: 48085
Poruke: 221
*.r62.logikom.net.

Sajt: www.geocities.com/predrag..

Profil

Re: Definicija funkcije

^{10.05.2005. u 06:53 - pre 243 meseci}

Uzmi prostiji primer

f(x)=x/x

Ta funkcija nije definisana za x=0 dok je lim f(x) kad x->0 jednako 1.
To proizilazi upravo iz pojma lim.

jer

f(1)=1
f(1/2)=1
f(1/4)=1
f(1/8)=1
....
....
....

x-ovi formiraju niz : 1, 1/2, 1/4, 1/8 ..... a to je niz sto tezzi 0
dok odgovarajucci y-i formiraju niz 1, 1, 1, 1, .... a to je niz koji tezzi 1

Zato je lim f(x) = 1 kad x->0

Prosto receno A=lim f(x) kad x->a znaci da kad x-ovi tezze broju a
odgovarajucci y-i tezze broju A.

No pitanje je da li znass sta znaci "niz tezzi nekom broju"?
Ovo je jedan od kljucnih pojmova u matematickoj analizi i trebalo bi malo visse vremena da se objasni a zavisi i od tvog matematickog backgrounda kojim recnikom bi ti to trebalo objasniti

tisuću lijepih žena posve nagih

Odgovor na temu

zi::
Igor Marinović
Manufaktura doo Internet inženjering
Palić

Član broj: 18090
Poruke: 642
*.manufacture.co.yu.

ICQ: 7715569
Sajt: www.marinowski.com

Profil

Re: Definicija funkcije

^{10.05.2005. u 12:19 - pre 243 meseci}

Ovo je poenta:

Citat:

No pitanje je da li znass sta znaci "niz tezzi nekom broju"?

Velika vecina njih, cak i onih na matematickom fakultetu, jednostavno ne moze da usvoji naizgled jednostavan pojam neprekidnosti, limesa. Otud pitanja poput ovih sto je sMRDo postavio.

Odgovor na temu

KPYU
Karan Predrag

Član broj: 36769
Poruke: 143
217.26.66.*

Profil

Re: Definicija funkcije

^{11.05.2005. u 00:52 - pre 243 meseci}

Ukolko je

Napominjem kod limesa imamo sledeće jednakosti:

Razume se ovde 0 nije stvarno 0, nego nešto što je skoro pa nula. Isto tako

je samo nešto jaaaako veliko.

Leibnitz je postavio nestandardnu analizu uvodeći infentizimale. Infentizimala je jaaako mala vrednost. Ne bi bilo ispravno smatrati je brojem. Pozitivna je, no ipak manja od bilo kojeg pozitivnog broja. Razume se ovo je jako plitko objašnjenje, koje ne bi držalo vodu ni pod kakvim ozbiljnijim ispitivanjima, ali intuitivno prihvatljivo. Nula iz prethodnog pasusa treba biti shvaćena kao infintezimala.

Idemo dalje. Još uvek ću pisati 0 ali čitajte je kao infintezimalu

Sledeći limesi nisu izračunljivi na prvu loptu (tj mogu se izračunati malo podrobnijom analizom)

Možda si čuo za izraz "nula drugog reda" ili "dvostruka nula" kod rešavanja kvadratnih jednačina. To se dobija kada je D=0, tj kada se naša kvad j-na može predstaviti na sledeći način

E, pa kod ovakvih limesa mora da se odredi stepen te nule, odnosno stepen beskonačnosti.

Odgovor na temu

peddja_stankovic
predrag stankovic
private
beograd

Član broj: 48085
Poruke: 221
*.r62.logikom.net.

Sajt: www.geocities.com/predrag..

Profil

Re: Definicija funkcije

^{11.05.2005. u 11:51 - pre 243 meseci}

kad smo vecc kod funkcija, da li neko zna primer iz fizike ili bilo ccega drugog da funkcija ima neotklonjiv prekid?

tisuću lijepih žena posve nagih

Odgovor na temu

zi::
Igor Marinović
Manufaktura doo Internet inženjering
Palić

Član broj: 18090
Poruke: 642
*.manufacture.co.yu.

ICQ: 7715569
Sajt: www.marinowski.com

Profil

Re: Definicija funkcije

^{11.05.2005. u 12:28 - pre 243 meseci}

Sta hoces zapravo da pitas? Primer iz zivota gde funkcija ima neotklonjiv prekid? Cuo sam da je probijanje zvucnog zida stvarno gadno, da model toga nije cak ni klase

, ali mozda se pogresno secam. Ako su lagali mene ...

Odgovor na temu

KPYU
Karan Predrag

Član broj: 36769
Poruke: 143
*.nspoint.net.

Profil

Re: Definicija funkcije

^{11.05.2005. u 13:48 - pre 243 meseci}

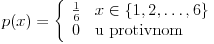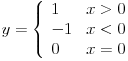
Ovo je funkcija sgn x

Ima neotklonjiv prekid u nuli. Ovo je prekid I reda, jer funkcija ima limes u nj okolini (zasebno levi & desni limes). Zato bi i mogo biti neotklonjiv (mada to nije, jer su levi i desni limes međusobom različiti).

Prekidi II & III reda ne mogu biti otklonjivi

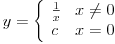
gde je c proizvoljan realan broj.

Ovo je prekid II reda jer limes f-je nije konačan.

Neki autori nazivaju prekidom III reda tačku u čijoj okolini f-ja nema nikakav limes. Kod drugih je to takođe prekid II vrste

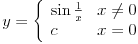
Ova dva poslednja primera sam namerno dodefinisao u nuli, da bih izbegao opštu zabludu. F-ja

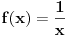
je NEPREKIDNA. Ona je, naime, neprekidna gde god je definisana.

Code:
Funkcija je prekidna u tački u kojoj je definisana, a nije neprekidna.

Kada, naprotiv govorimo o tačkama prekida, uzimamo zatvorenje domena. Tako ćemo za gorenavedenu funkciju f(x) reći da je neprekidna, a ipak da je tačka x=0 tačka prekida II vrste.

Dakle Neprekidnost f-je ne zavisi od njene vredosti u tački, nego od vrednosti uokolini te tačke

Za kraj LaGranževa funkcija

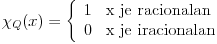
koja je prekidna u svakoj svojoj tački.

PS
Postoji još brdo jedno neprekidnih funkcija, koje srećemo u svakodnevnom životu. Npr celi deo (tj [x]), zatim gomila funkcija raspodele koje srećemo u verovatnoći kao

Odgovor na temu

peddja_stankovic
predrag stankovic
private
beograd

Član broj: 48085
Poruke: 221
*.r62.logikom.net.

Sajt: www.geocities.com/predrag..

Profil

Re: Definicija funkcije

^{11.05.2005. u 14:04 - pre 243 meseci}

KPYU,

Nisi me razumeo. Na primer, put je neprekidna funkcija brzine i vremena
S(v,t)=v*t.
Hoccu recci da li u prirodi postoje funkcijeske zavisnosti koje nisu neprekidne - taccnije koje funkcije za kontinualni argument imaju skok - diskontinuitet u vrednosti.

PS
Sto se ticce proboja zvuccnog zida - intuitivno mislim da je takodje neprekidna ali mozzda nam neki kompetentni sagovornik razjasni diluemu. Mogucce je da u trenutku proboja zvucnog zida amplituda ima velike ali ipak konacne vrednosti.

_{[Ovu poruku je menjao peddja_stankovic dana 11.05.2005. u 15:15 GMT+1]}

tisuću lijepih žena posve nagih

Odgovor na temu

peddja_stankovic
predrag stankovic
private
beograd

Član broj: 48085
Poruke: 221
*.r62.logikom.net.

Sajt: www.geocities.com/predrag..

Profil

Re: Definicija funkcije

^{11.05.2005. u 14:10 - pre 243 meseci}

I jos jedno pitanje da ne zaboravim, ovo nisam nashao u literaturi.
U definiciji limesa niza, da li epsilon mozze /mora biti iz R/Q.

tisuću lijepih žena posve nagih

Odgovor na temu

peddja_stankovic
predrag stankovic
private
beograd

Član broj: 48085
Poruke: 221
*.r62.logikom.net.

Sajt: www.geocities.com/predrag..

Profil

Re: Definicija funkcije

^{11.05.2005. u 14:56 - pre 243 meseci}

odnosno [x],

Da, ovo ti je lep primer. Funkcija raspodele verovatnocce bacanja kockice. Dodushe recc je o diskretnom procesu ali ipak ga opisuje funkcija koja ima neotklonjiv prekid bash kao sto sam se pitao.

tisuću lijepih žena posve nagih

Odgovor na temu

KPYU
Karan Predrag

Član broj: 36769
Poruke: 143
*.nspoint.net.

Profil

Re: Definicija funkcije

^{11.05.2005. u 15:53 - pre 243 meseci}

Ne idem redom.

Po def

je iz R, jer ni Q ni R\Q nisu kompletni.

Svaki put kada "u prirodi" dolazi do nagle promene nekog stanja, javlja se skok:
sudari čestica, kidanja etc

Napominjem, taj prekid se može, npr videti, preko veličina koje izražavaju lokalne promene, tj koje su "izražljive" preko izvoda.

Npr kod sudara, (recimo kugla o ivicu bilijarskog stola), ukupan put je neprekidna funkcija, ali brzina ima prekid. Ukoliko bismo usporili sam sudar i posmatrali ga stvarno neprekidno, oko ove "prekidne" promene brzine, mogli bismo još diskutovati, no ubrzanje (izvod brzine po vremenu), definitivno ima prekid.

Proboj zvučnog zida možemo shavtiti kao "kidanje" vazdušnog sloja ispred letelice.

Odgovor na temu

peddja_stankovic
predrag stankovic
private
beograd

Član broj: 48085
Poruke: 221
*.r62.logikom.net.

Sajt: www.geocities.com/predrag..

Profil

Re: Definicija funkcije

^{11.05.2005. u 17:10 - pre 243 meseci}

Da li se mozze iskonstruisati kontra-primer koji bi oborio pretpostavku da

mozze biti iz Q.

Deluje razumno na prvi pogled da na primer kod sudara dve metalne kugle ili udarca bilijarske o bilijarski sto dolazi do diskontinuiteta u ubrzanju. Ali, valjda se kugla u veoma kratkom vremenu zaustavi i usled "crne kutije" zvane zakon akcije i reakcije odbije. Ja mislim da tu ipak nemamo diskontinuitet tipa sgn(x).
(Ili ja razmishljam ko mali Perica?)

tisuću lijepih žena posve nagih

Odgovor na temu

KPYU
Karan Predrag

Član broj: 36769
Poruke: 143
*.nspoint.net.

Profil

Re: Definicija funkcije

^{11.05.2005. u 20:02 - pre 243 meseci}

Eh, problemi kontinuiteta i diskontinuiteta....

Ljudskom oku film može delovati kao neprekidan sled događaja, mada je prekidan (mislim 26 frame/sec)

Zahvaljujući kvantnoj fizici možemo videti da je stvarnost diskontinuitetnog karaktera. Mi je, naravno, takvom ne doživljavamo.

No, sa druge strane, postoji takva stvar kao što je limes niza. Ukoliko budemo precizniji videćemo da ceo skup Q možemo predstavit u obliku niza. Limes po skupu Q bi tada bio limes niza. No, t nije limes f-je.

Hajneova definicija neprekidnosti f-je daje spoj limesa f-je i limesa niza. Naime
Hajne

postoji akko za svaki niz y_n takav da

postoji limes niza

i svi takvi limesi nizova su međusobom jednaki.

No, ja sam najzad dokontao šta ti kažeš. Ti kažeš da

.

A to je tačno. Naravno u ovom slučaju.

Odgovor na temu

peddja_stankovic
predrag stankovic
private
beograd

Član broj: 48085
Poruke: 221
*.r62.logikom.net.

Sajt: www.geocities.com/predrag..

Profil

Re: Definicija funkcije

^{11.05.2005. u 20:18 - pre 243 meseci}

Bravo

To sam hteo

Jel to neka teorema

PS
Priznajem da sam ponekad nedovoljno precizan, da ne kazzem nejasan.

tisuću lijepih žena posve nagih

Odgovor na temu

peddja_stankovic
predrag stankovic
private
beograd

Član broj: 48085
Poruke: 221
*.r62.logikom.net.

Sajt: www.geocities.com/predrag..

Profil

Re: Definicija funkcije

^{11.05.2005. u 21:02 - pre 243 meseci}

Pa red bi bilo da za neupuccene damo definiciju granicne vrednosti niza

Dakle

tisuću lijepih žena posve nagih

Odgovor na temu

zi::
Igor Marinović
Manufaktura doo Internet inženjering
Palić

Član broj: 18090
Poruke: 642
*.tippnet.co.yu.

ICQ: 7715569
Sajt: www.marinowski.com

Profil

Re: Definicija funkcije

^{11.05.2005. u 21:15 - pre 243 meseci}

Skup Q je redak. Imao sam sreću biti na Kurepinom predavanju kada je pričao o racionalnim brojevima: kada bi kiša padala samo po racionalnim brojevima, većina realne osi bi ostala suha. Srećom, Q je dovoljno gust da imamo dovoljno racionalnih brojeva makar koliko mali interval izabrali. Zato mislim (to je samo osećaj, nisam 100% siguran) da je svejedno da li je

iz Q ili iz R. Uostalom, mi

zadajemo, a na njega odgovaramo sa

u

igri u definiciji neprekidnosti.

Inače, da budemo potpuno precizni:

Citat:

KPYU:
Dakle Neprekidnost f-je ne zavisi od njene vredosti u tački, nego od vrednosti u okolini te tačke

Ovo nije tačno. Ja bih rekao da neprekidnost funkcije ne zavisi samo od njene vrednosti u tački, nego i od vrednosti u okolini te tačke.

Trivijalan protuprimer: funkcija

ima vrednost 1 svugde osim u nuli, gde je

. Ova funkcija nije neprekidna u nuli (pogledajte definiciju), a kada bi zavisila samo od okoline nule, onda bi bila neprekidna.

Naravno, kada se računa limes ne pita se sama tačka, nego samo okolina tačke pa je limes ove funkcije u nuli jednak 1.

Odgovor na temu

KPYU
Karan Predrag

Član broj: 36769
Poruke: 143
*.nspoint.net.

Profil

Re: Definicija funkcije

^{12.05.2005. u 00:30 - pre 243 meseci}

@zi::

Slažem se. Poenta mog posta nije bila da neprekidnost u tački ne zavisi od vrednosti u tački, nego i od ponašanja f-je u okolini. Ukoliko f-ja NIJE definisana u samoj tački, tu ne možemo, naravno, govoriti o vrednosti u samoj tački.

Btw Q nije redak, no gust. Jeste gust, ali nije kompletan. Prepun je rupica, no svugde ga ima.

@peddja_stankovic

Činjenica se ultra-lako dokazuje time što na proizvoljnom intervalu

imamo kako racionalnih, tako i iracionalnih vrednosti, bez obzira na to da li je

racionalno ili ne.

PS

Izvinjavam se što sam tako lupetao, a da nisam prethodno dobro pročitao post. No, ko se poslednji smeje, slabo kapira viceve.

Odgovor na temu

zi::
Igor Marinović
Manufaktura doo Internet inženjering
Palić

Član broj: 18090
Poruke: 642
*.manufacture.co.yu.

ICQ: 7715569
Sajt: www.marinowski.com

Profil

Re: Definicija funkcije

^{12.05.2005. u 08:12 - pre 243 meseci}

Jeste, pogrešno sam se izrazio da je Q redak. Hteo sam reći da je R mnogo gušći :)

Nisam siguran da li smo pomogli sMRDi, verujem da mu tek sada ništa nije jasno :)

Odgovor na temu

Svetle
Svetle Frost
Beograd

Član broj: 45794
Poruke: 35
*.ptt.yu.

Profil

Re: Definicija funkcije

^{12.05.2005. u 18:13 - pre 242 meseci}

Da bi postavljacu teme ista bilo jasno evo da probam da malo sistematizujem napisano.

Tvoja funkcija, kao sto si primetio, nije definisana u -2 i 2. Ono sto je jako bitno je to da su -2 i 2 tacke nagomilavanja skupa A=domen funkcije. To znaci da u svakom intervalu oko -2 ili 2 ima beskonacno mnogo tacaka iz A.
Znaci, kad se govori o limesu f-je u nekoj tacki ta tacka mora da bude tacka nagomilavanja domena f-je. Opste, sto se tice limesa f-je u tacki a, ona moze (sama vrednost f(a) ne utice na limes), ali i ne mora biti definisana u a. U ovom zadatku treba da ispitas ponasanje f-je oko tacaka -2 i 2 (moze se desiti da su levi i desni limes razliciti – to je slucaj u tacki -2).

Posto je pomenuta neprekidnost f-je, a cija definicija naizgled lici na limes, postoje bitne razlike. Kod neprekidnosti f-je u tacki a mora biti definisano f(a). Dalje, tacka a ne mora biti tacka nagomilavanja domena f-je. Najprostiji primer je izolovana tacka domena (u nekoj njenoj okolini nema drugih tacaka domena osim nje same). Tu nema smisla govoriti o limesu, a ona je u toj tacki neprekidna.

Sto se tice tacaka prekida f-je. Tacka a iz domena je tacka prekida f-je ako f nije neprekidno u toj tacki (KPYU je pisao o tome, a trebalo bi jos jednom naglasiti). Tacka u kojoj f-ja nije definisana ne moze biti njena tacka prekida (pa neka je i tacka nagomilavanja domena). A od tacaka nagomilavanja domena tacke prekida su one tacke kod kojih limes ne postoji, limes nije jednak vrednosti f-je u toj tacki.

Jos jedan dodatak. Hajne je definisao limes f-je preko limesa niza, koja je ekvivalentna sa Kosijevom preko okolina.

Ne mesati neprekidnost i limes je moj savet svima koji uce analizu.

Odgovor na temu

KPYU
Karan Predrag

Član broj: 36769
Poruke: 143
*.nspoint.net.

Profil

Re: Definicija funkcije

^{12.05.2005. u 21:30 - pre 242 meseci}

Ne bih se složio. Tačno: u izolovanim tačkama, f-ja je po definiciji neprekidna. Ali, kad god imamo tačku domena koja nije izolovana, teško je izvući bilo šta bez limesa. Ovakvi zadaci su najčešći. Ljudima takvi zadaci trebaju. Podsetiću: limesi f-je zadate preko elementarnih f-ja se traže u rubovima domena.

Retko kome se traži neprekidnost funkcije koja nije zadata na podskupu Rⁿ. Uopšteno posmatramo levi i desni limes. Oni mogu biti konačni (prekid I vrste), beskonačni (II vrste), ili da uopšte ne postoje (III vrste). Prekidi I vrste mogu biti otklonjivi i neotklonjivi.

Hajne jeste definisao limes f-je preko limesa niza, ali ne zaboravimo, za svaki niz...

Neprekidnost se definiše u proizvoljnom topološkom prostoru. Nikakva metrika nam nije potrebna za neprekidnost. Kao uostalom ni za limes. Ta dva pojma su jako blisko povezana.

Odgovor na temu

[es] :: Matematika :: Definicija funkcije

Strane: 1 2

[ Pregleda: 10540 | Odgovora: 23 ] > FB > Twit

Srodne teme

26.03.2002. definicija
05.05.2003. Condition funkcije u Windows-u ?
14.03.2004. ExtraNet pojam i definicija ???
29.09.2004. brisanje odredjenih definicija?
02.10.2004. Kako naci redosled kojim su pozivane funkcije?
19.09.2005. Definisanje funkcija..... etc?
04.11.2005. Implicitno pozivanje ReleaseMutex funkcije
17.11.2005. Potrebna pomoc oko minimuma funkcije
24.11.2005. Pomoc kod izvodjenja relacije
13.03.2006. Dvije funkcije ;-)

Navigacija

Lista poslednjih: 16, 32, 64, 128 poruka.