Citat:
maximus_1:
2.Najmanji cijeli broj m takav da funkcija
y=(m-2)x2+m+2+3x ima pozitivne vrijednosti na cijeloj domeni
da bi ova kvadratna funkcija bila pozitivna na celom domenu, tj. da parabola čija je to jednačina bude u koordinatnom sistemu "iznad" x ose, treba da budu ispunjena dva uslova,
prvo da nema presek sa x osom, što znači da nema realnih nula (dovoljno je da odgovarajuća kvadratna jednačina nema realnih rešenja, što praktično znači da joj je diskriminanta uvek strogo negativna)
i da koeficijent uz kvadratni član bude pozitivan.
To se svodi na dve nejednačine
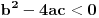
i

gde su a, b i c odgovarajući koeficijenti, u tvom slučaju a=m-2, b=3 i c=m+2, a rešenje zadatka će, naravno, biti najmanji ceo broj koji zadovoljava obe.