[es] - Aritmeticki i geometrijski niz

kupina

Član broj: 46571
Poruke: 33
*.208.EUnet.yu.

Profil

^{10.02.2005. u 23:12 - pre 245 meseci}

Treba odrediti 4 broja od kojih prva 3 cine aritmeticki, a poslednja 3 geometrijski niz s tim da je zbir srednjih za dva manji od zbira krajnjih a proizvod poslednja dva je 8.

Resila sam nesto slicno kad je dat zbir unutrasnjih i krajnjih ali kako ovde doci do resenja?

Odgovor na temu

peddja_stankovic
predrag stankovic
private
beograd

Član broj: 48085
Poruke: 221
*.r62.logikom.net.

Sajt: www.geocities.com/predrag..

Profil

Re: Aritmeticki i geometrijski niz

^{11.02.2005. u 07:45 - pre 245 meseci}

Neka su to brojevi a, b, c, i d

uslov da su prva tri aritm. prog ................ b=(a+c)/2
uslov da su poslednja tri geom. prog ......... c^2=b*d
trecci uslov ......................................... b+c=a+d-2
cetvrti uslov ........................................ c*d=8

to su 4 jednacine sa 4 nepoznate. Kad ubacim u math cad iz za sada nepoznatog razloga ne dobija resenje, aloi uz malo muke se dobija da je to niz 12 8 4 2

za sada toliko, ako treba detaljnije oko resavanja sistema mogu da poradim na tome u toku dana

pedja

tisuću lijepih žena posve nagih

Odgovor na temu

KPYU
Karan Predrag

Član broj: 36769
Poruke: 143
*.nspoint.net.

Profil

Re: Aritmeticki i geometrijski niz

^{11.02.2005. u 17:31 - pre 245 meseci}

Ukoliko ima aritmetički niz a₁, a₂, ..., a_n, znaš da je a₂=a₁+d, ...,a_n=a₁+ (n-1)d. Sada ti ceo niz zavisi samo od 2 promenljive:a₁ i d. Ovakav sistem nije preterano lak za rešavanje. Lakši sistem dobijaš kad uvedeš smenu

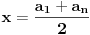
i (u zavisnosti n)

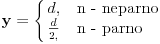
Za n =3: a₂=x, y=d. Tj a₁=x-y, a₂=x,a₃=x+y
Dakle imamo niz x-y, x, x+y, z. 3 zadnja člana su geometrijski niz. tj xz=(x+y)². Dalje x+x+y=x-y+z-2, (x+y)z=8.
Zamenimo z =x+2y+2 u prvu jednačinu.2x=y². Sad sve to zamenimo u treću jednačinu:

.
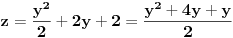
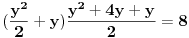
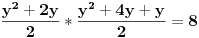
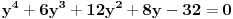
Ovde imamo 2 realna rešenja.
Jedno rešenje je y=-4. Tada x=8, z=2. Brojevi su 12, 8, 4, 2.
Drugo rešenje je iracionalno i nije lepo, te ga ovde neću pisati, jer ovo ne radim za ocenu, niti za pare.

_{[Ovu poruku je menjao KPYU dana 15.02.2005. u 07:06 GMT+1]}

_{[Ovu poruku je menjao KPYU dana 15.02.2005. u 07:07 GMT+1]}

_{[Ovu poruku je menjao KPYU dana 15.02.2005. u 07:09 GMT+1]}

_{[Ovu poruku je menjao KPYU dana 15.02.2005. u 07:10 GMT+1]}

_{[Ovu poruku je menjao KPYU dana 15.02.2005. u 07:11 GMT+1]}

Odgovor na temu

kupina

Član broj: 46571
Poruke: 33
*.54.EUnet.yu.

Profil

Re: Aritmeticki i geometrijski niz

^{14.02.2005. u 20:51 - pre 245 meseci}

pedja, molila bih resavanje ovog sistema detaljnije

KPYU, sve to u redu sto si ti radio, ali resavanjem koje jednacine konacno kao resenje dobija y=-4?

Odgovor na temu

peddja_stankovic
predrag stankovic
private
beograd

Član broj: 48085
Poruke: 221
*.r62.logikom.net.

Sajt: www.geocities.com/predrag..

Profil

Re: Aritmeticki i geometrijski niz

^{15.02.2005. u 17:11 - pre 245 meseci}

Imam resenje u word formatu valjda cce ovo da bude ok?

Pedja

tisuću lijepih žena posve nagih

Prikačeni fajlovi

kupina.rtf - 71.84k

Odgovor na temu